Билет 1.Аксиоматика ординалистской теории.

Ординалистская теория - упорядочение потребителем своих предпочтений относительно благ. невозможно измерить предельную полезность, так как потребитель измеряет не полезность отдельных благ, а полезность наборов благ. Измеримости поддается только порядок предпочтения наборов благ. Потребитель систематизирует выбор набора благ по уровню удовлетворения. Подобная систематизация дает представление о предпочтениях потребителей в отношении набора благ. Однако она не дает представления о различиях удовлетворения данными наборами благ. То есть с практической точки зрения потребитель может сказать, какой набор он предпочитает другому, но не может определить, насколько один набор предпочтительнее другого.

1. Аксиома полной (совершенной) упорядоченности. Потребитель способен упорядочить все возможные наборы товаров с помощью отношений предпочтения (у) и безразличия (~). Это означает, что для любой пары товарных наборов А и В потребитель может указать, что либо А > В (А предпочтительнее, чем В), либо В > А (В предпочтительнее, чем А), либо А ~ В (А и В равноценны).

2. Аксиома транзитивности. Если А > В > С, или А ~ В> С, или А > В ~ С, то А > С. Эта аксиома гарантирует согласованность предпочтений. Она, например, исключает возможность следующей ситуации: А > В, В > С и одновременно С > А.

Аксиома транзитивности содержит и еще одно утверждение, а именно: если А ~ В и В ~ С, то А ~ С. 3.

Аксиома ненасыщения. Если набор А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А > В. Таким образом, предполагается, что увеличение потребления любого товара при фиксированных объемах потребления других товаров улучшает положение потребителя.

4. Аксиома независимости потребителя. Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими.

Это прежде всего означает, что потребителю не знакомы чувства зависти и сострадания. В принципе и от этой аксиомы можно отказаться, что иногда и делается, в частности при анализе процессов потребления, сопровождающихся внешними эффектами и внешними затратами.

При порядковом подходе используются кривые и карта безразличия. Кривая безразличия ≈ это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Если заполнить двухмерную плоскость кривыми безразличия так плотно, как это возможно, получим карту безразличия.

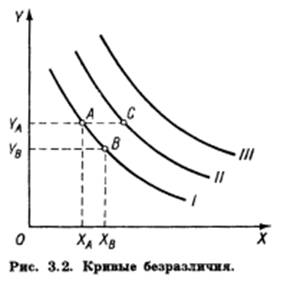
На рис. 3.2 товарный набор А включает Х_А единиц товара X и Y_А единиц товара Y, товарный набор В включает Х_B единиц товара X и Y_B единиц товара Y. Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной и той же кривой безразличия.

Кривые безразличия обладают следующими свойствами.

А. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные для данного потребителя наборы товаров. Рассмотрим на рис. 3.2 кривые безразличия I и II. Набор С содержит такое же количество товара Y, что и набор А. Но набор С включает в себя большее количество товара X. Из аксиомы о ненасыщении следует, что С > А. Все наборы, лежащие на кривой безразличия I, с точки зрения нашего потребителя равноценны. То же относится и ко всем наборам, лежащим на кривой II. Из аксиомы о транзитивности следует, что любой набор, лежащий на кривой II, для нашего потребителя предпочтительнее любого набора, лежащего на кривой I.

Б. Кривые безразличия имеют отрицательный наклон. Пусть дана некоторая точка А (рис. 3.3), характеризующая определенную комбинацию товаров. Проведем через нее две взаимно перпендикулярные прямые. Очевидно, что все точки, лежащие в III квадранте, соответствуют большим, а все точки, лежащие в I квадранте, ≈ меньшим количествам товаров X и Y, чем точка А. В соответствии с аксиомой ненасыщения точки, лежащие в III квадранте, более предпочтительны, а лежащие в I квадранте ≈ менее предпочтительны, чем А. Следовательно, точки, безразличные А, например С, или В, или D, или G, должны находиться либо во II, либо в IV квадранте. И значит, кривая безразличия должна иметь отрицательный наклон.

В. Кривые безразличия никогда не пересекаются. Предположим противное. Пусть кривые безразличия I и II на рис. 3.4 пересеклись в точке В. Из аксиомы о ненасыщении следует, что А > С. Наборы В и С лежат на одной кривой безразличия I. Поэтому В ~ С. Наборы А и В лежат на одной кривой безразличия II. Поэтому А ~ В. Из аксиомы о транзитивности следует, что А ~ С. Однако не могут одновременно быть А > С и А ~ С. Следовательно, кривые безразличия не могут пересекаться.

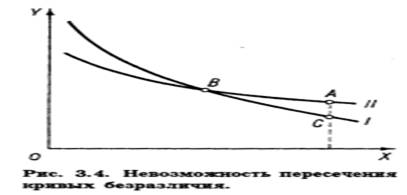
Заметим, что в отличие от непересекающихся прямых, которые должны быть параллельными, кривые могут не пересекаться и не будучи параллельными.

Г. Кривая безразличия может быть проведена через любую точку пространства товаров. Говорят еще, что кривая безразличия не имеет "толщины". Это свойство любых линий в Евклидовой геометрии, оно является безусловно определенной идеализацией, абстракцией реального мира. Чтобы сделать его более реалистичным, необходимо при выборе единицы измерения товаров учитывать порог восприятия.

Д. Кривые безразличия выпуклы к началу координат. Это свойство в отличие от ранее перечисленных не может быть выведено непосредственно из аксиом рационального поведения. Оно просто отражает принцип диверсификации потребления.

Основным рабочим понятием порядковой теории полезности является предельная норма замещения (MRS; marginal rate of substitution).

Предельной нормой замещения благом X блага Y(MRS_XY) называют количество блага Y, которое должно быть сокращено "в обмен" на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:

Поскольку отношение DY/DX по определению отрицательно, минус, вводимый перед правой частью, делает значение нормы замещения положительным.

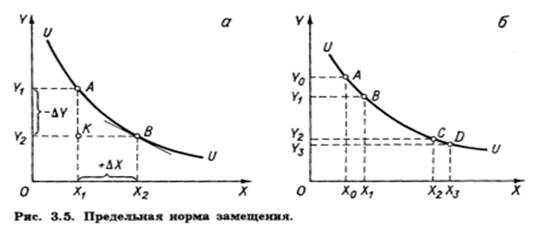
Пусть потребитель безразличен между наборами А и В (рис. 3.5, а). Значит, норма, по которой он согласен замещать благо Y благом X, оставаясь при этом на одной и той же кривой безразличия, составит

(OY₁ - OY₂)/(OY₁ - OY₂) = - DY/DX = -AK/KB

По мере приближения точки А к точке В отношение АК/КВ будет приближаться к наклону касательной в точке В. В пределе в окрестностях В наклон кривой (или касательной) в этой точке и есть предельная норма замещения:

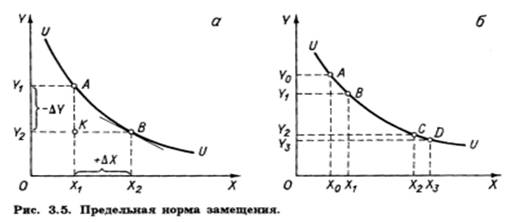
Предельная норма замещения может принимать различные значения, она может быть равна нулю, может быть неизменной или меняться при движении вдоль кривой безразличия. В случае выпуклости к началу координат, как на рис. 3.5, MRS убывает по мере замещения одного блага другим, т.е. потребитель соглашается отдавать все меньшее количество замещаемого блага за одно и то же количество замещающего (аналог убывающей предельной полезности). Так, на рис. 3.5,б потребитель, находясь в точке А, готов уступить Y₀Y₁ блага Y взамен приращения блага X на X₀X₁. Однако, располагая набором С, он за равновеликое приращение блага X (X₂X₃ = X₀X₁) согласится уступить лишь Y₂Y₃ блага Y, что меньше Y₀Y_1. Для двух совершенно взаимозаменяемых товаров MRS = const. В этом случае кривые безразличия вырождаются в прямые линии (линия U₁U₁ на рис. 3.6). Обычно такие товары рассматриваются как один товар.

2. Бюджетное ограничение. Оптимум потребителя.

потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Но он ограничен в своих средствах. Далеко не всякий товарный набор ему доступен. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия. Потребитель заинтересован в конечном итоге получить наилучшее из возможных сочетаний потребления в этих периодах, что на графике соответствовало бы наивысшей кривой безразличия. Однако бюджетное ограничение требует, чтобы потребитель в итоге оказался на или ниже линии бюджетного ограничения, поскольку эта линия показывает все средства, которыми он располагает. линию бюджетного ограничения пересекают несколько кривых безразличия. Наивысшая кривая безразличия, которой может достичь потребитель, не выходя за рамки бюджетного ограничения, есть кривая, которая лишь касается линии ограничения. Точка, в которой эта кривая соприкасается с линией бюджетного ограничения точка О (для обозначения оптимума) и есть наилучшее сочетание потребления в первоми во втором периоде, доступное при данном бюджетном ограничении. В точке оптимума наклон кривой безразличия совпадает с наклоном линии бюджетного ограничения. Кривая безразличия является касательной к линии бюджетного ограничения

3. Влияние изменения цен на выбор потребителя. Линия «цена-потребление» и кривая спроса.

Если изменение дохода при постоянных ценах выражалось в параллельных сдвигах бюджетной линии (рис. 1), то изменение цены на один из товаров при постоянстве дохода и цены другого товара будет выглядеть как поворот бюджетной линии (рис. 10). Таким образом, каждому значению цены товара Х будет соответствовать своя бюджетная линия, а каждой бюджетной линии - своя точка касания с какой-нибудь кривой безразличия. Соединив все эти точки выбора, как в предыдущем разделе, мы получим линию цена-потребление товара X.

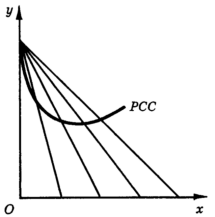
Рис. 10. Построение линии цена-потребление товара Х.

4. влияние изменений дохода на выбор потребителя. Лини «доход-потребление» и кривые Энглея. Обобщенный закон Энгеля.

Если одновременно снижается Рх и Ру, то это означает увеличение реального дохода потребителя и равномерное смещение бюджетной линии вправо. С1, С2, С3, С4- параметры рыночного равновесия при различных уровнях дохода. Соединив их, получим линию «доход-потребление».
Линия «доход-потребление» связывает точки равновесия и показывает, как потребление товаров х и у изменяется с ростом дохода.

Для нормальных благ линия «доход-потребление» имеет положительный наклон, для некачественных товаров – отрицательный наклон, для нейтральных товаров она вертикальна.
Зависимость объема спроса на благо от дохода потребителя в графическом виде называется кривой Энгеля.

5. эффекты дохода и замещения по Дж. Хиксу.

Эффект дохода возникает, поскольку изменение цены данного товара увеличивает (при снижении цены) или уменьшает (при повышении цены) реальный доход или покупательную способность, потребителя. Эффект замещения (замены) возникает в результате относительного изменения цен. Эффект замещения способствует росту потребления относительно подешевевшего товара, тогда как эффект дохода может стимулировать и увеличение, и сокращение потребления товара или быть нейтральным. Для того чтобы определить эффект замены, нужно элиминировать влияние эффекта дохода. Или наоборот, чтобы определить эффект дохода, нужно элиминировать эффект замены. Согласно Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, т.е. позволяющие достигнуть одной и той же кривой безразличия, представляют одинаковый уровень реального дохода.

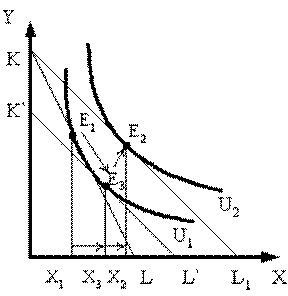
Разложение общего эффекта изменения цены на эффект дохода и эффект замены по Хиксу показано на рис.8.1 Бюджетная линия KL соответствует денежному доходу I и ценам Рх и Ру. Ее касание с кривой безразличия U₁ определяет оптимум потребителя Е₁, которому соответствует объем потребления товара в количестве X₁. В случае снижения цены X до Рх₁ и неизменном денежном доходе I бюджетная прямая займет положение KL₁. Она касается более высокой кривой безразличия U₂ в точке Е₂, которой соответствует потребление товара X в объеме Х₂.

Таким образом, общий результат снижения цены товара X выражается в увеличении его потребления с X₁ до Х₂.

Определим, каким должен был бы быть денежный доход потребителя, чтобы при изменившемся соотношении цен обеспечить ему прежний уровень удовлетворения. Для этого проведем вспомогательную бюджетную прямую K'L', параллельную линии KL₁ (т.е. отражающую новое соотношение цен), так, чтобы она касалась кривой безразличия U₁ (т.е. обеспечивала бы прежний уровень удовлетворения). Отметим точку касания Е₃ и соответствующий объем потребления товара X₃.

Заметим, что при переходе от первоначального к дополнительному (расчетному) оптимуму (от Е₁ к Е₃) реальный доход потребителя не меняется, он остается на прежней кривой безразличия U₁. Значит, сдвиг от Е₁ к Е₃ и характеризует эффект замены товара Y относительно подешевевшим товаром X. Он равен разности (Х₃–X₁). Следовательно, эффект дохода составит (Х₂ - Х₃).

Заметим также, что в результате действия эффекта дохода потребление обоих товаров в точке Е₂ выше, чем в точке Е₃.

Такое же разложение общего эффекта может быть выполнено и для случая, когда цена товара повышается.

6. компенсированный спрос.

обыкновенная, или кривая спроса Маршалла построена на основе кривой цена-потребление, полученной в результате вращения бюджетной прямой вокруг точки К. Такая обыкновенная кривая спроса отражает совместное влияние на объем спроса и эффекта замены, и эффекта дохода.

Напротив, скомпенсированная кривая спроса отражает влияние на объем спроса лишь эффекта замены. Она может быть построена, исходя из предпосылки о том, что при повышении цены какого-либо товара или группы товаров реальный доход потребителей остается неизменным; это может быть достигнуто путем компенсации роста цен либо прямым увеличением номинальных доходов, либо увеличением располагаемого дохода за счет сокращения налогов, либо какими-то другими способами.

7. Эффекты дохода и замещения по Е. Слуцкому.

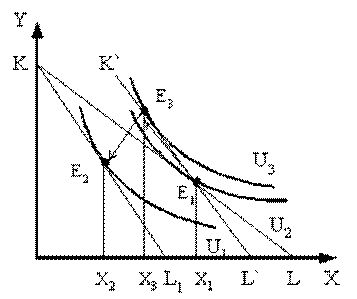
Подход Слуцкого к разложению общего результата изменения цены на эффект дохода и эффект замены отличается от подхода Хикса трактовкой реального дохода. Выделение эффекта дохода достигается определением такого его уровня, который обеспечил бы потребителю возможность приобрести после изменения цен тот же самый набор товаров, что и до изменения, а не сохранить прежний уровень удовлетворения, как это предполагается в модели Хикса.

Поэтому на рис. 8.2 вспомогательная бюджетная прямая KL, параллельная KL₁, проводится не как касательная к прежней кривой безразличия U₁, а строго через точку Е₁, соответствующую оптимальному набору товаров X и У при прежнем соотношении цен. Очевидно, она окажется касательной к более высокой, чем U₁, кривой безразличия U₃, что означает и возможность достигнуть (в случае полной компенсации потребителю – падения его покупательной способности) более высокого уровня удовлетворения, чем при использовании модели Хикса. Таким образом, общий результат повышения цены товара X (Х₁-Х₃) разлагается на эффект замены (X₁-Х₃) и эффект дохода (Х₃-Х₂). Заметим, что движение от Е₁ к Е₂ происходит не вдоль кривой безразличия, а вдоль вспомогательной бюджетной прямой K'L'.

8. уравнение Слуцкого

— уравнение, смысл которого состоит в том, что изменение спроса на некоторый товар при повышении или снижении его цены складывается из влияния непосредственного изменения спроса и косвенного влияния в результате переключения спроса на другие товары.

Изменение
спроса

эффект
изменения
дохода

эффект
замещения

Левая часть (4.26) представляет не что иное, как коэффициент эластичности спроса на товар X ≈ e_X.

Первое слагаемое правой части можно представить как k_Xe_I, где k_X = XP_X/I ≈ доля расходов на товар X в общих расходах покупателя I, а e_I ≈ коэффициент эластичности спроса на товар X по доходу.

Второе слагаемое правой части характеризует эластичность спроса на товар X при неизменном реальном доходе, обозначим ее коэффициент -

Таким образом, мы можем записать уравнение Слуцкого (3.17) в коэффициентах эластичности:

e_{X = -kXeI +}_ex

В то время как эффект замещения должен быть всегда отрицателен — противоположен направлению изменения цены, эффект дохода может действовать в обоих направлениях. Следовательно, общий эффект может быть положительным или отрицательным. Однако, в случае нормального товара эффект замещения и эффект дохода действуют в одном и том же направлении. Рост цены означает, что спрос сократится вследствие действия эффекта замещения. Поскольку мы рассматриваем ситуацию роста цены, это подразумевает снижение покупательной способности, что для нормального товара означает сокращение спроса.

С другой стороны, если мы рассматриваем товар низшей категории, может случиться так, что эффект дохода перевесит эффект замещения, так что общее изменение спроса, связанное с изменением цены, в действительности окажется положительным. В этом случае мы имели бы

9. Компенсирующая и эквивалентная вариации дохода.

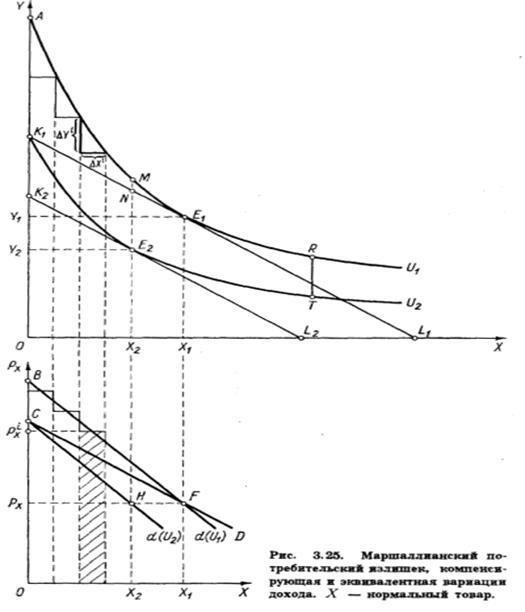
эквивалентная вариация дохода, поскольку она представляет собой изменение дохода, которое, с точки зрения полезности, эквивалентно изменению цены. Предположим, бюджетная линия занимает положение K₁L₁. Длина отрезка OK₁ равна доходу потребителя I. Наклон бюджетной линии равен ≈ Р_X. Допустим, что первоначально потребитель имеет возможность приобретать неограниченное количество товара X по цене Р_X- Он выбирает товарный набор, соответствующий точке E₁. Этот набор включает X₁ единиц товара X. Сумма расходов на прочие товары равна OY₁. Сумма расходов на X₁ единиц товара X равна Y₁K₁.

Предположим теперь, что потребитель лишен возможности покупать товар X. Тем самым он оказывается в точке K₁. Какую дополнительную сумму дохода ему нужно предоставить, чтобы его благосостояние не изменилось по сравнению с первоначальным положением? Поскольку точка А лежит на той же кривой безразличия, что и точка K₁, необходимая дополнительная сумма дохода равна K₁А. Эта величина называется компенсирующей вариацией дохода. Обозначим ее V_c.

Снова предположим, что потребитель находится в точке E₁. Какой максимальной суммой дохода он готов пожертвовать ради того, чтобы его не лишали возможности покупать товар X? Проведем вспомогательную бюджетную линию K₂L₂, параллельную линии K₁L₁ и касающуюся той линии безразличия, которая проходит через точку K₁. Потребитель не согласится пожертвовать суммой, превышающей K₂K₁, иначе кривая безразличия, проходящая через K₁, оказывается для него недостижимой. Любая "жертва", меньшая, чем K₂K₁, позволяет потребителю увеличить свое благосостояние по сравнению с положением K₁. Следовательно, максимальная сумма дохода, которой готов пожертвовать потребитель ради того, чтобы его не лишали возможности покупать товар X, равна K₂K₁. Эта величина называется эквивалентной вариацией дохода.¹ Обозначим ее V_e.

Следует обратить внимание на то, что в определении V_c за основу принимается начальная кривая безразличия, в определении V_e за основу принимается последующая кривая безразличия (в нашем случае кривая безразличия, проходящая через точку K₁).

10. Взаимосвязь между различными показателями выгоды потребителя.

1)Излишек потребителя может по-прежнему служить разумной мерой благосостояния потребителя в целом ряде применений. Ошибки в измерении кривых спроса обычно перевешивают ошибки, связанные с приближенными подсчетами, сопутствующими использованию излишка потребителя в качестве меры благосостояния.

Может оказаться, однако, что для некоторых применений такой приближенный подсчет недостаточен. Предположим, что мы рассматриваем ситуацию, изображенную на рис.12.1. На рис.A показана компенсирующая вариация дохода (CV), а на рис.B — эквивалентная вариация дохода (EV). Здесь потребителю первоначально заданы какие-то цены (), и он потребляет некий набор (х₁^*,х₂^*). Затем цена товара 1 возрастает с p₁^* до , и потребитель переходит к потреблению набора . Насколько большой ущерб благосостоянию потребителя наносит это изменение цены?

14-4

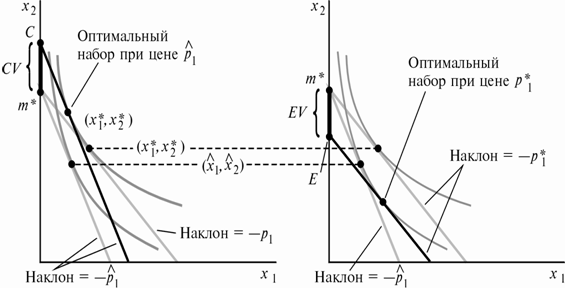
A B

Рисунок 12.1 Компенсирующая и эквивалентная вариации дохода.

Один из способов ответа на данный вопрос состоит в том, чтобы спросить, сколько денег следует дать потребителю после изменения цены, чтобы его благосостояние осталось точно таким же, каким оно было до изменения цены. Применительно к графической иллюстрации, мы спрашиваем, как сильно вверх мы должны сдвинуть новую бюджетную линию, чтобы она стала касательной к кривой безразличия, проходящей через точку исходного потребления (х₁^*,х₂^*). Изменение дохода, необходимое для того, чтобы потребитель вновь оказался на исходной кривой безразличия, называется компенсирующей вариацией дохода, так как оно представляет собой такое изменение дохода, которое как раз компенсирует потребителю влияние изменения цены. Компенсирующая вариация дохода показывает, сколько денег правительство должно было бы добавить потребителю, если бы хотело в точности компенсировать ему изменение цены. Другой способ измерить влияние изменения цены в денежных единицах состоит в том, чтобы спросить, сколько денег следовало бы забрать у потребителя до изменения цены, чтобы его благосостояние было точно таким же, каким оно стало после изменения цены. Эта мера называется эквивалентной вариацией дохода, поскольку она представляет собой изменение дохода, которое, с точки зрения полезности, эквивалентно изменению цены. Применительно к рис.12.1 мы спрашиваем, как сильно вниз мы должны сдвинуть исходную бюджетную линию, чтобы как раз коснуться кривой безразличия, проходящей через новый потребительский набор. Эквивалентная вариация дохода показывает максимальную величину дохода, с которой потребитель готов был бы расстаться, чтобы избежать изменения цены.

Вообще, та сумма денег, которую потребитель был бы готов заплатить, чтобы избежать изменения цены, как правило, отличается от той суммы денег, которую следовало бы выплатить потребителю, чтобы компенсировать ему изменение цены. В конце концов, при разных комбинациях цен стоимость доллара для потребителя различна, поскольку на него он может приобрести разные величины потребления. Выражаясь языком геометрии, компенсирующая и эквивалентная вариации дохода — не что иное как два различных способа измерить то, "как далеко отстоят друг от друга" две кривых безразличия. В каждом из случаев мы измеряем расстояние между двумя кривыми безразличия расстоянием между касательными к ним. Вообще, эта мера расстояния будет зависеть от наклона касательных — то есть, от выбранных нами цен, определяющих наклон бюджетных линий. Однако, компенсирующая и эквивалентная вариации дохода одинаковы в одном важном случае — при квазилинейной функции полезности. В этом случае кривые безразличия параллельны, так что расстояние между кривыми безразличия, как показано на рис.12.1, остается одним и тем же, независимо от того, в какой точке его измеряют. В случае квазилинейной функции полезности компенсирующая вариация дохода, эквивалентная вариация дохода и изменение избытка потребителя дают одну и ту же меру денежной стоимости изменения цены.

11.Потрребительский выбор с учетом начального запаса.

Начальный запас – это то количество благ, которое потребитель имеет еще до начала анализа в жестко фиксированном виде. Далее анализ проведен для ситуации финансового рынка, где представлены два игрока - кредитор и заемщик. (Кредитор – субъект (юридическое или физическое лицо), предоставляющий ссуду и имеющий право на это основе требовать от дебитора ее возврата или исполнения других обязательств. Заемщик – получатель кредита, займа, принимающий на себя обязательство, гарантирующий возвращение полученных средств, оплату предоставленного кредита). Для них главную роль играет ставка процента. В случае же классических товаров изменяться будет цена одного из них. Кроме того, об анализе для классических товаров можно прочитать в начале ответа на следующий вопрос. Итак, пусть процентная ставка растет. Данный случай легче проанализировать, используя бюджетное ограничение, выраженное не через текущую стоимость, а через будущую стоимость. С позиций бюджетного ограничения, выраженного через будущую стоимость, повышение процентной ставки - то же самое, что повышение цены сегодняшнего потребления по сравнению с ценой завтрашнего потребления. Выписав уравнение Слуцкого, получаем

(?) (-) (?) (+)

10-4

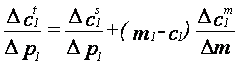
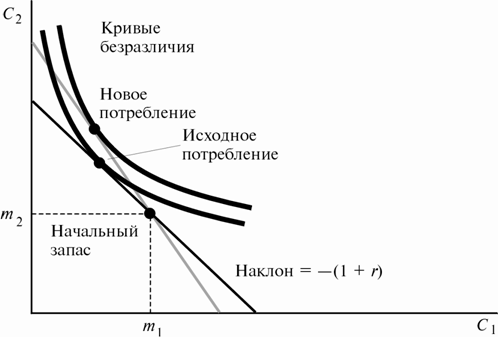
Рисунок 10.4 Потребительский выбор с учетом начального запаса.

Действие эффекта замещения, как всегда, направлено в сторону, противоположную изменению цены. В данном случае цена потребления в период 1 растет, следовательно, эффект замещения говорит нам о том, что в первом периоде потребитель должен потреблять меньше. В этом заключается смысл знака "минус", стоящего под эффектом замещения. Допустим, что потребление в рассматриваемом периоде есть нормальный товар, так что самый последний член - изменение потребления с изменением дохода - будет величиной положительной. Записываем под последним членом знак "плюс". Теперь знак всего выражения будет зависеть от знака (). Если рассматриваемое лицо - заемщик, этот член будет величиной отрицательной и поэтому выражение в целом, несомненно, будет отрицательным - для заемщика рост процентной ставки должен уменьшать сегодняшнее потребление.

Почему это происходит? В случае повышения процентной ставки всегда действует эффект замещения, вызывающий уменьшение сегодняшнего потребления. Для заемщика повышение процентной ставки означает, что завтра ему придется платить более высокий процент. Это побуждает его меньше занимать и, тем самым, меньше потреблять в первом периоде. Для кредитора рассматриваемый эффект неоднозначен. Общий эффект есть сумма отрицательного эффекта замещения и положительного эффекта дохода. С точки зрения кредитора, рост процентной ставки может принести ему такой большой дополнительный дохода, что он захочет даже увеличить свое потребление в первом периоде.

10-5

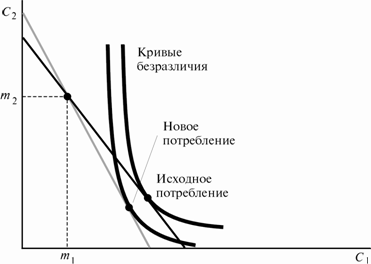
Рисунок 10.5

Последствия изменения процентных ставок не так уж загадочны. Как и при любом другом изменении цены, в этом случае действуют эффект дохода и эффект замещения. Однако, без такого инструмента анализа, как уравнение Слуцкого, позволяющего обособить различные эффекты, соответствующие изменения распутать трудно. С помощью же этого инструмента вычленение указанных эффектов производится достаточно просто.

12.Концепция выявленных предпочтений.

Прежде всего следует принять одно допущение. Суть его в том, что все предпочтения, каковы бы они ни были, являются строго выпуклыми. Рассмотрим рис.7.1, на котором изображены набор спроса потребителя (x₁, x₂) и другой, произвольно взятый набор, (y₁, y₂), лежащий под бюджетной линией потребителя. Предположим, что мы причисляем данного потребителя к ранее рассматривавшейся нами категории потребителей, оптимизирующих свою полезность. Что можно сказать о предпочтениях потребителя в отношении двух указанных товарных наборов?

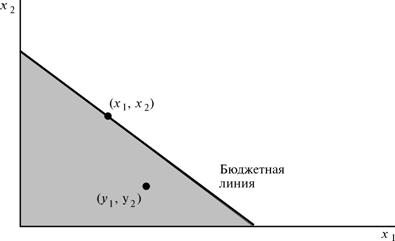
Рисунок 7.1 Концепция выявленных предпочтений.

Что ж, можно сказать, что набор (y₁, y₂), безусловно, может быть куплен при данном бюджетном ограничении — потребитель мог бы приобрести его, если бы захотел, и после этого у него даже остались бы деньги. Поскольку (x₁, x₂) — оптимальный набор, он должен быть лучше любого другого набора, доступного потребителю. Следовательно, он должен быть, в частности, лучше набора (y₁, y₂). На рис.7.1 все наборы, расположенные в заштрихованной области под бюджетной линией, выявленно хуже набора спроса (x₁, x₂). Это потому, что они могли быть выбраны, но были отвергнуты в пользу набора (x₁, x₂).

Пусть (x₁, x₂) — набор, приобретаемый по ценам (p₁, p₂) при доходе потребителя, равном m. Каков смысл утверждения о том, что набор (y₁, y₂) доступен при данных ценах и доходе? Оно означает просто, что (y₁, y₂) удовлетворяет бюджетному ограничению

p₁y₁ + p₂y₂ £ m.

Поскольку набор (x₁, x₂) фактически куплен при заданном бюджетном ограничении, он должен удовлетворять бюджетному ограничению со знаком равенства

p₁x₁ + p₂x₂ = m.

Соединим оба этих уравнения. Тот факт, что (y₁, y₂) доступен потребителю при бюджетном ограничении, заданном ценами и доходом (p₁, p₂, m), означает, что

p₁x₁ + p₂x₂ ³ p₁y₁ + p₂y₂.

Если приведенное выше неравенство удовлетворяется и (y1, y2) является набором, отличным от (x₁, x₂), мы говорим, что набор (x₁, x₂) прямо выявленно предпочитается набору (y₁, y₂). Принцип выявленного предпочтения. Пусть (x₁, x₂) есть товарный набор, выбранный при ценах (p₁, p₂), а (y₁, y₂) — какой-то другой товарный набор, такой, что

p₁x₁ + p₂x₂ ³ p₁y₁ + p₂y₂

Тогда, если потребитель выбирает наиболее предпочитаемый набор из числа доступных, то должно соблюдаться (x₁, x₂) f (y₁, y₂).

Пусть теперь нам известно, что (y₁, y₂) — набор спроса при ценах (q₁, q₂) и что (y₁, y₂) выявленно предпочитается какому-то другому набору (z₁, z₂). Т.е.

q₁y₁ + q₂y₂ ³ q₁z1 + q₂z₂

Тогда нам известно, что (x₁, x₂) f (y₁, y₂) и что (y₁, y₂) f (z₁, z₂). На основании аксиомы транзитивности предпочтений можно заключить, что (x₁, x₂) f (z₁, z₂).

Эта аргументация проиллюстрирована рис. 7.2. Выявленное предпочтение и транзитивность говорят о том, что для потребителя, сделавшего выбор, представленный этим рисунком, набор (x₁, x₂) должен быть лучше набора (z₁, z₂).

Естественно было бы утверждать, что в данном случае набор (x₁, x₂) косвенно выявленно предпочитается набору (z₁, z₂). Конечно, "цепочка" наблюдаемых случаев выбора может включать более трех наборов: если набор A прямо выявленно предпочитается набору B, набор B — набору C, набор C — набору D... и т.д. до, скажем, M, то набор A косвенно выявленно предпочитается набору M. Цепочка прямых сравнений может быть любой длины.

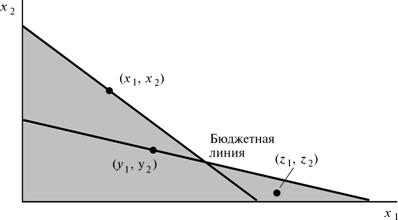
Рисунок 7.2 Косвенно выявленные предпочтения.

Слабая аксиома выявленных предпочтений (Weak Axiom of Revealed Preference — WARP). Если набор (x₁, x₂) прямо выявленно предпочитается набору (y₁, y₂) и рассматриваемые наборы не тождественны, то не может быть так, чтобы набор (y₁, y₂) прямо выявленно предпочитался набору (x1, x2). Иными словами, если набор (x₁, x₂) покупается по ценам (p₁, p₂), а отличный от него набор (y₁, y₂) покупается по ценам (q₁, q₂), то в случае, когда

p₁x₁ + p₂x₂ ³ p₁y₁ + p₂y₂,

не должно быть так, чтобы

q₁y₁ + q₂y₂ ³ q₁x₁ + q₂x₂.

Можно сформулировать это и словами: если набор y доступен, когда покупается набор x, то набор x не должен быть доступен, когда покупается набор y.

Сильная аксиома выявленных предпочтений (SARP). Если набор (x₁, x₂) выявленно предпочитается набору (y₁, y₂) (прямо или косвенно) и набор (y₁, y₂) отличен от набора (x₁, x₂), то набор (y₁, y₂) не может прямо или косвенно предпочитаться набору (x₁, x₂).

13.Производственные функции. Изокванты: их виды и характеристики. Эффект масштаба производства . Технический прогресс.

Вводимые в производство ресурсы называются факторами производства. Они часто подразделяются на крупные категории, такие, как земля, труд, капитал и сырьевые материалы. Капитальные товары — это такие вводимые в производство ресурсы, которые сами являются товарами, произведенными в процессе производства. В основном капитальные товары — это того или иного рода машины: тракторы, компьютеры, а также здания и пр. Иногда понятие "капитал" применяется для описания тех денег, которые используются для открытия предприятия или его финансовой поддержки. Но правильнее использовать для этого термин "финансовый капитал", а для обозначения факторов производства, созданных в процессе производства, — термин "капитальные товары", или "физический капитал". Будем считать, что вводимые ресурсы и выпуск измеряются единицами потока: определенное количество труда в неделю и определенное число часов работы машин в неделю производят определенную величину выпуска в неделю.

Природа налагает на фирмы технологические ограничения: лишь некоторые комбинации вводимых ресурсов представляют собой практически осуществимые способы производства данного объема выпуска, и фирма должна ограничивать свой выбор технологически выполнимыми производственными программами. Простейший способ описания выполнимых производственных программ — это составление их перечня. Иными словами, мы можем составить список всех комбинаций вводимых ресурсов и выпусков, являющихся технологически достижимыми. Множество всех комбинаций вводимых ресурсов и выпусков, которые охватывают технологически достижимый способ производства, называется производственным множеством. Предположим, например, что у нас имеется только один вводимый ресурс, в количестве x, и только один выпуск, в количестве y. Тогда производственное множество может иметь форму, показанную на рис.17.1. Утверждение, что некоторая точка (x, y) принадлежит производственному множеству, означает просто следующее утверждение: имея количество x данного вводимого ресурса, технологически возможно произвести выпуск в объеме y. Производственное множество показывает возможные для данной фирмы варианты технологического выбора. Поскольку фирма оплачивает вводимые ресурсы, имеет смысл ограничиться изучением максимально возможного выпуска при данном уровне вводимого ресурса. Это — граница производственного множества, представленного на рис.17.1. Функция, описывающая границу этого множества, известна как производственная функция. Она показывает максимально возможный выпуск, который может быть получен из данного количества вводимого ресурса. Разумеется, концепция производственной функции в равной степени применима и тогда, когда имеется несколько вводимых ресурсов. Если, например, мы рассматриваем случай двух вводимых ресурсов, производственная функция f(x₁, x₂) будет показывать максимальный объем выпуска y, который мы могли бы получить, если бы у нас имелось x₁ единиц фактора 1 и x₂ единиц фактора 2. Существует удобный способ изображения производственных взаимосвязей для случая двух факторов производства, известный как изокванта. Изокванта — это множество всех возможных комбинаций факторов 1 и 2, которые как раз достаточны для производства данного объема выпуска.

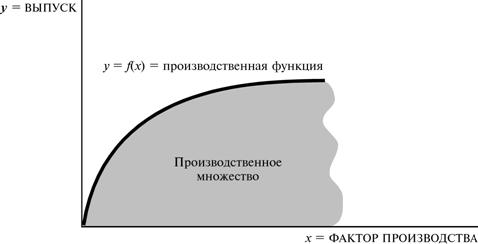
Рисунок 17.1 Производственное множество и производственная функция.

Изокванты подобны кривым безразличия. Но при этом изокванты обозначаются не уровнями полезности, а объемами выпуска, которые могут быть произведены с помощью соответствующих комбинаций факторов. Поэтому обозначение изоквант задано технологией и не имеет той произвольной природы, которая присуща обозначению полезности.

В коротком периоде всегда имеются какие-то факторы производства, количество которых задано и неизменно. Предположим, что использование фактора 2, скажем, в коротком периоде неизменно и равно . Тогда соответствующая производственная функция для короткого периода есть f(x₁,). Мы можем представить функциональную взаимосвязь между выпуском и x₁ графически, как на рис.17.5.

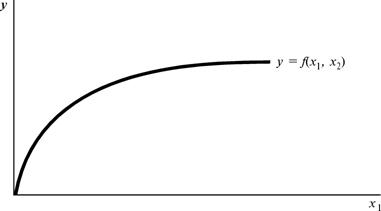
Рисунок 17.5 Производственная функция.

На рисунке краткосрочная производственная функция становится все более и более пологой по мере возрастания количества фактора 1. Здесь мы сталкиваемся с действием закона убывания предельного продукта. . Рассмотрим конкретный пример такой ситуации, связанный с сельским хозяйством. Один человек на одном акре земли может произвести 100 бушелей зерна. Если привлечь еще одного человека и сохранить количество земли без изменений, можно получить 200 бушелей зерна, так что в этом случае предельный продукт добавочного работника равен 100. Будем продолжать увеличивать число работников, обрабатывающих этот акр земли. Добавление каждого работника может увеличивать производимый выпуск, но со временем добавочное количество зерна, производимое добавочным работником, станет меньше 100 бушелей. После добавления четырех или пяти человек дополнительный выпуск на работника снизится до 90, 80, 70 ...или даже меньшего количества бушелей зерна. Если на этом одном акре земли столпятся сотни работников, то прибавление добавочного работника может вызвать даже падение выпуска! Как и при приготовлении бульона, когда поваров слишком много, может пострадать результат. Таким образом, по мере увеличения количества фактора производства, мы ожидаем, как правило, убывания предельного продукта данного фактора. Это явление называется законом убывания предельного продукта (более распространенные названия этого закона: "закон убывающей отдачи" и "закон убывающей предельной производительности факторов". Конечно, вполне может случиться, что на графике будет иметься некая первоначальная область возрастания предельного дохода, в которой по мере увеличения количества фактора 1 предельный продукт этого фактора растет. В случае, когда фермер увеличивает число работников, может случиться так, что добавление первых нескольких работников вызовет увеличение выпуска, потому что им удастся провести эффективное разделение труда, и т.п. Однако при заданном постоянном количестве земли с течением времени предельный продукт труда будет снижаться.

Вместо того чтобы увеличивать количество одного применяемого фактора, сохраняя количество другого фактора неизменным, будем увеличивать количество всех факторов, от которых зависит производственная функция. Другими словами, умножим количество всех факторов на некий постоянный множитель: например, будем использовать в два раза больше как фактора 1, так и фактора 2. Какой объем выпуска мы получим, если будем использовать в два раза больше каждого фактора? При наиболее вероятном исходе, мы получим вдвое больший объем выпуска. Этот случай называют случаем постоянной отдачи от масштаба. В терминах производственной функции это означает, что удвоение количества каждого фактора производства приносит удвоение объема выпуска. Математически для случая двух факторов это можно выразить в виде

2f(x₁, x₂) = f(2x₁, 2x₂).

Вообще, если мы увеличиваем количество всех факторов в одно и то же число раз t, постоянная отдача от масштаба означает, что мы должны получить в t раз больший объем выпуска:

tf(x₁, x₂) = f(tx₁, tx₂).

Мы считаем этот исход вероятным по следующей причине: как правило, фирма должна быть способна повторить то, что она делала раньше. Если у фирмы имеется в два раза больше каждого фактора производства, то она может просто открыть рядом два завода и в результате получить вдвое больший выпуск. Имея в три раза больше каждого фактора, она может открыть три завода и т.д.

Обратите внимание на то, что технология вполне может характеризоваться постоянной отдачей от масштаба и при этом убыванием предельного продукта каждого фактора. Отдача от масштаба описывает то, что происходит при увеличении количества всех факторов, в то время как убывание предельного продукта описывает то, что происходит при увеличении количества одного из факторов и сохранении неизменным количества остальных факторов.

Постоянная отдача от масштаба в силу приведенного довода о повторении результата является наиболее "естественным" случаем, но вовсе не означает, что невозможны другие исходы. Например, могло бы случиться так, что при умножении количеств обоих факторов на какой-то множитель t мы получили бы более чем в t раз больший выпуск. Этот случай называют случаем возрастающей отдачи от масштаба. Математически возрастающая отдача от масштаба означает, что

f(tx₁, tx₂) > tf(x₁, x₂).

для всех t > 1. Какая технология дает пример возрастающей отдачи от масштаба? Один из удачных примеров такого рода — технология производства нефтепровода. Удваивая диаметр трубы, мы используем вдвое больше материалов, но площадь поперечного сечения трубы увеличивается в четыре раза. Поэтому мы, скорее всего, сможем прокачать через нее более чем вдвое больше нефти. (Разумеется, в этом примере нам не следует заходить слишком далеко. Если продолжать удваивать диаметр трубы, она в конце концов рухнет под тяжестью собственного веса. Возрастающая отдача от масштаба обычно наблюдается лишь в определенном диапазоне выпуска.)

Следует рассмотреть также случай убывающей отдачи от масштаба, при которой

f(tx₁, tx₂) < tf(x₁, x₂) для всех t > 1.

Этот случай несколько специфичен. Если от удвоения количества каждого фактора мы получаем менее, чем вдвое больший выпуск, мы, должно быть, делаем что-то не так. В конце концов мы ведь могли бы просто повторить то, что делали раньше!

Убывающая отдача от масштаба обычно возникает из-за того, что мы забыли учесть какой-то фактор производства. Если у нас вдвое больше каждого фактора, за исключением одного, мы уже не сможем в точности повторить то, что делали раньше, так что нет причин ожидать, что мы получим выпуск, вдвое больший. Убывающая отдача от масштаба есть, на самом деле, явление, наблюдающееся в коротком периоде, когда количество какого-либо фактора сохраняется постоянным. Разумеется, одна и та же технология может характеризоваться различной отдачей от масштаба при разных уровнях производства. Вполне может случиться, что при более низких объемах производства технология характеризуется возрастающей отдачей от масштаба — по мере умножения количеств факторов на какую-то малую величину t выпуск возрастает более чем в t раз. Позднее, для более высоких уровней выпуска, увеличение количеств факторов в t раз может привести к увеличению выпуска как раз в t раз.

В результате технического прогресса возможен рост производства, который заключается в появлении новых, технически более эффективных способов производства. Эти новые способы должны быть учтены в производственной функции, тогда как старые должны быть исключены из нее. Графически технический прогресс может быть отражен сдвигом вниз изокванты и, возможно, изменением ее конфигурации. Сдвинутая вниз изокванта характеризует тот же объем выпуска, что и старая, но теперь этот объем выпуска может быть достигнут за счет применения меньшего количества капитала и труда. Сдвиг изокванты может сопровождаться изменением ее конфигурации, что означает изменение соотношения применяемых ресурсов. В связи с этим различают три типа технического прогресса: капиталоинтенсивный (трудосберегающий), трудоинтенсивный (капиталосберегающий) и нейтральный. Технический прогресс называется капиталоинтенсивным, если при движении вдоль линии спостоянным соотношением К/L, предельная норма замещения одного фактора другим снижается. Это означает, что технически й прогресс сопровождается опережающим ростом предельного продукта капитала по сравнению с трудом. Трудоинтенсивный технический прогресс сопровождается опережающим ростом предельного продукта труда по сравнению с предельным продуктом капитала. Наклон изокванты при приближении к началу координат становится все более пологим относительно оси К.

Наконец, нейтральным называется технический прогресс, в результате которого происходит пропорциональное увеличение обоих факторов, но предельная норма замещения остается неизменной. Не меняется при этом и наклон изокванты, под воздействием технического прогресса она смещается параллельно самой себе.

14.Траектория расширения производства и условный спрос на ресурсы.

Пусть минимизирующая издержки фирма увеличивает выпуск. Она переходит на более высокие изокванты, используя экономически эффективные способы производства.

[Примечание Экономически эффективными способами производства являются такие конфигурации ресурсов, при которых изокванта и изокоста касаются, и точка касания является в задаче максимизации выпуска Q=f(K,L) при заданном ограничении на ресурсы (С=rK+wL) точкой максимума целевой функции Q=f(K,L), а в задаче минимизации издержек (С=rK+wL) при заданном объеме выпуска Q=f(K,L) она является точкой минимума. Соединяя точки касания изоквант и изокост, мы получаем линию, характеризующую траекторию расширения производства. Поскольку рост выпуска требует увеличения количества всех ресурсов, траектория расширения производства имеет положительный наклон. В случае неизменной отдачи от масштаба это будет прямая линия, при убывающей отдаче или возрастающей отдаче она может быть прямой или зигзагообразной, в зависимости от того, является производственная функция однородной или неоднородной. Если соотношение цен факторов производства изменится, изменится и траектория расширения производства, поскольку экономически эффективными станут иные способы производства. Сочетания ресурсов, характеризующие экономически эффективные способы производства, формируют условный, или производный, спрос на ресурсы. Это спрос на ресурсы, необходимом для определенного объема выпуска с минимальными издержками. Траектория расширения производства характеризует условный спрос на ресурсы во всех возможных значениях выпуска. При изменении соотношения цен на ресурсы условный спрос изменяется в соответствии с изменением траектории расширения производства. Условный спрос есть функция от цен ресурсов и объема выпуска:

D(усл)=f(r,w,Q).

Насколько интенсивными будут изменения условного спроса на ресурсы при изменениях цен на ресурсы, зависит от эластичности замещения:

(*)

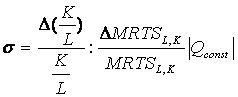Поскольку в точке оптимума (минимум издержек) MRTS=, коэффициент эластичности замещения можно представить в виде * только с заменой MRTS на w/r. Коэффициент показывает, на сколько процентов изменится капиталовооруженность труда в экономически эффективном способе производства при изменении отношения цен на ресурсы (w/r) на 1%.

15.Предложение конкурентной фирмы в коротком и длительных периодах. Квазипостоянные издержки. Излишек производителя в коротком идлительном периоде.

Применим факты, выясненные нами в отношении кривых издержек, для того чтобы вычислить кривую предложения конкурентной фирмы. По определению, конкурентная фирма игнорирует свое влияние на рыночную цену. Таким образом, задачу максимизации, стоящую перед конкурентной фирмой, можно записать:

max py — c(y).

Это говорит просто о том, что конкурентная фирма хочет максимизировать свою прибыль: разность между общим доходом py и издержками c(y).

Какой объем выпуска решит производить конкурентная фирма? Ответ: она будет действовать в точке, где предельный доход равен предельным издержкам, — там, где добавочный доход, приносимый еще одной единицей выпуска, как раз равен добавочным издержкам производства еще одной единицы выпуска. Если бы данное условие не удовлетворялось, фирма всегда могла бы увеличить свою прибыль путем изменения своего объема выпуска.

В случае конкурентной фирмы предельный доход есть просто цена. Чтобы увидеть это, спросим себя, сколько добавочного дохода получит конкурентная фирма, увеличив выпуск на Dy. Мы получим

DR = pDy,

поскольку согласно нашей гипотезе p не изменяется. Поэтому добавочный доход на единицу выпуска задается формулой

DR/Dy = p,

представляющей собой выражение для предельного дохода.

Таким образом, конкурентная фирма выберет объем выпуска y в точке, где предельные издержки как раз равны рыночной цене. В условных обозначениях:

p = MC(y).

Мы хотим найти объем выпуска, максимизирующий прибыль при данной рыночной цене p. Если при каком-то объеме выпуска y цена больше предельных издержек, фирма может увеличить свою прибыль, чуть увеличив выпуск. Ведь превышение ценой предельных издержек означает, что

p — .

Поэтому увеличение выпуска на Dy означает, что

pDy — .

Упростив это неравенство, мы находим, что

pDy —Dc > 0,

а это означает, что прирост общего дохода от добавочного выпуска превышает прирост издержек. Следовательно, прибыль при этом должна увеличиться.

Аналогичные рассуждения можно провести и для случая, когда цена ниже предельных издержек. Тогда сокращение выпуска приведет к увеличению прибыли, поскольку потерянный при этом доход более, чем компенсируется сократившимися издержками.

Таким образом, при оптимальном объеме выпуска фирма должна производить в точке, где цена равна предельным издержкам. Каков бы ни был уровень рыночной цены p, фирма выберет объем выпуска y, соответствующий условию p = MC(y). Поэтому кривая предельных издержек конкурентной фирмы есть в точности ее кривая предложения. Или, другими словами, рыночная цена есть в точности предельные издержки до тех пор, пока каждая фирма производит объем выпуска, максимизирующий ее прибыль.

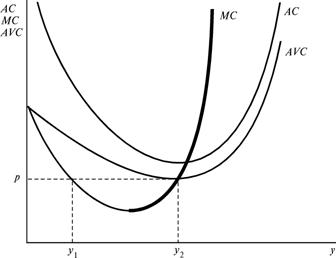
Рисунок 21.2 Предельные издержки и предложение.

В данных рассуждениях предполагается, что выгодно производить что-то. Но в конце концов самым выгодным для фирмы могло бы оказаться и производство нулевого выпуска. Поскольку всегда имеется возможность произвести нулевой объем выпуска, мы должны сравнить точку предполагаемой максимизации прибыли с точкой нулевого производства.

Если фирма производит нулевой выпуск, она по-прежнему должна оплачивать постоянные издержки F. Следовательно, прибыль от производства нуля единиц выпуска равна просто —F. Прибыль от производства объема выпуска y есть py — c_v(y) — F. Фирме выгоднее прекратить деятельность, когда

—F > py —c_v(y) —F,

т.е. когда "прибыль" от нулевого производства и просто оплаты постоянных издержек превышает прибыль от производства в точке, где цена равна предельным издержкам. Преобразование этого неравенства дает нам условие закрытия:

Если средние переменные издержки больше p, фирме выгоднее производить ноль единиц выпуска. В этом есть смысл, поскольку это условие говорит о том, что общий доход от продажи выпуска y не покрывает даже переменных издержек производства c_v(y). В этом случае фирме лучше выйти из бизнеса. Если она не будет производить ничего, она потеряет постоянные издержки, но она потеряла бы даже больше, если бы продолжала производить.

Эти рассуждения показывают, что только те части кривой предельных издержек, которые лежат над кривой средних переменных издержек, могут состоять из точек, принадлежащих кривой предложения. Если точка, в которой цена равна предельным издержкам, находится под кривой средних переменных издержек, то в оптимуме фирма предпочтет производить нуль единиц выпуска.

Теперь перед нами вырисовывается картина кривой предложения, подобная изображенной на рис.21.3. Конкурентная фирма производит в той части кривой предельных издержек, которая является восходящей и лежит над кривой средних переменных издержек.

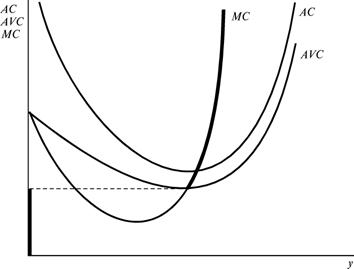
Рисунок 21.3 Средние переменные издержки и предложение.

Кривая долгосрочного предложения конкурентной фирмы строится на основании тех же принципов, что и кривая ее краткосрочного предложения. Поскольку по условию оптимальности P=MC , кривая предложения в долгосрочном периоде совпадает с кривой долгосрочных предельных издержек. Но в долгосрочном периоде все издержки фирмы являются переменными. Если цена становится ниже минимальных средних издержек, то фирма может избавиться от убытков, просто прекратив выпуск. Поэтому кривая долгосрочного предложения фирмы совпадает с кривой долгосрочных предельных издержек только на участке, лежащем не ниже минимума средних издержек, при P>=minAC. Квазипостоянные издержки — это издержки, которые тоже не зависят от объема выпуска, но должны оплачиваться только при условии производства фирмой положительного объема выпуска.

В длительном периоде по определению постоянных издержек не бывает, однако вполне могут существовать квазипостоянные издержки. Если началу производства какого-то объема выпуска должна предшествовать затрата какой-то постоянной суммы, то можно говорить о наличии квазипостоянных издержек.

При заданной рыночной цене мы можем теперь найти оптимальную точку функционирования фирмы, воспользовавшись условием p = MC(y). Зная оптимальную точку функционирования фирмы, можно подсчитать прибыль фирмы. На рис.21.4 площадь прямоугольника есть не что иное, как p*y*, или общий доход. Площадь y*AC(y*) представляет общие издержки, так как

Прибыль есть просто разность этих двух площадей.

До этого излишек производителя определялся как площадь слева от кривой предложения по аналогии с излишком потребителя, представленным площадью слева от кривой спроса. Оказывается, излишек производителя тесно связан с прибылью фирмы. Точнее, излишек производителя равен общему доходу за вычетом переменных издержек, или, что то же самое, сумме прибыли и постоянных издержек:

Прибыль = py — c_v(y) — F

Излишек производителя = py — c_v.(y).

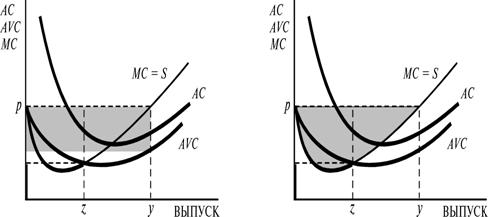
Наиболее непосредственный способ измерения излишка производителя заключается в подсчете разности площади прямоугольника дохода и площади прямоугольника y^*AVC(y^*), как на рис.21.5A. Однако имеются и другие способы измерения излишка производителя на основе использования самой кривой предельных издержек.

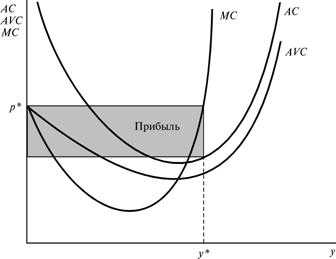
Рисунок 21.4 Прибыль.

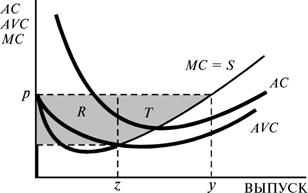
Площадь под кривой предельных издержек измеряет общие переменные издержки. Это верно, потому что площадь под кривой предельных издержек есть издержки производства первой единицы выпуска плюс издержки производства второй единицы выпуска плюс и т.д. Поэтому чтобы получить излишек производителя, можно вычесть площадь под кривой предельных издержек из прямоугольника общего дохода и получить площадь, представленную на рис.21.5B. Наконец, можно соединить оба способа измерения излишка производителя. Вплоть до точки, в которой предельные издержки равны средним переменным издержкам, можно использовать определение через площадь прямоугольника, а затем воспользоваться площадью над кривой предельных издержек, как показано на рис.21.5C. Этот способ наиболее удобен для большинства приложений, поскольку излишек производителя здесь выступает просто как площадь слева от кривой предложения.

А Общий доход — переменные издержки B Площадь над кривой MC

С Площадь слева от кривой предложения

Рисунок 21.5 Излишек производителя. На рис.A показан прямоугольник, измеряющий разность общего дохода и переменных издержек. На рис.B показана площадь над кривой предельных издержек. На рис.C до точки выпуска z излишек производителя измеряется с помощью прямоугольника (площадь R), а затем для его измерения используется площадь над кривой предельных издержек (площадь T).

max py — c(y).

Это говорит просто о том, что конкурентная фирма хочет максимизировать свою прибыль: разность между общим доходом py и издержками c(y). Какой объем выпуска решит производить конкурентная фирма? Ответ: она будет действовать в точке, где предельный доход равен предельным издержкам, — там, где добавочный доход, приносимый еще одной единицей выпуска, как раз равен добавочным издержкам производства еще одной единицы выпуска. Если бы данное условие не удовлетворялось, фирма всегда могла бы увеличить свою прибыль путем изменения своего объема выпуска.

DR = pDy,

DR/Dy = p,