16.Принцип максимизации выпуска и минимизации издержек.

 

Пусть нам дана конкретная технология производства продукта:

Q=KL

а также мы имеем стоимостное ограничение на ресурсы:

C=rK+wL,

где r – арендная плата за оборудование, а w – ставка заработной платы. Тогда данная задача формулируется так:

(максимизация выпуска)

(при заданном ограничении)

Т.к. это задача на условный экстремум (есть целевая функция, есть уравнение ограничения), то можно выписать функцию Лагранжа:

F(K,L,)= KL+(C-rK-wL)

Выпишем условия первого порядка:

Имеем систему из трех уравнений с тремя неизвестными. Для удобства решения разделим первое уравнение на второе.

Из этой системы находим K и L, т.е. в данном случае такую конфигурацию ресурсов, при которой достигается максимальный выпуск.

K=

L=

Q=()()=

K и L есть в данном случае функции спроса на ресурсы, зависящие от C, r, и w. Величина Q есть в данном случае максимальный выпуск, которого достигает фирма в точке (K,L)=(,). Q есть функция условного предложения фирмы.

Предположим, что у нас имеется два фактора производства с ценами w₁Ошибка! Не указан аргумент ключа. и w₂Ошибка! Не указан аргумент ключа. и мы хотим найти самый дешевый способ производства заданного объема выпуска y. Если обозначить используемые количества каждого из двух факторов через x₁ и x₂Ошибка! Не указан аргумент ключа., а производственную функцию для фирмы — через f(x₁, x₂)Ошибка! Не указан аргумент ключа.Ошибка! Не указан аргумент ключа., то эту задачу можно записать в виде

 

min w₁x₁ + w₂x₂

                                                    x₁, x₂Ошибка! Не указан аргумент ключа.

 

 при f(x₁, x₂)Ошибка! Не указан аргумент ключа. = y.

При проведении подобного рода анализа следует сделать те же предупреждения, что и в предыдущей главе: убедитесь, что вы включили в подсчет издержек все издержки производства и что все измерения производятся в совместимом временном масштабе.

Решение этой задачи минимизации издержек — величина минимальных издержек, необходимых для достижения определенного объема выпуска, — будет зависеть от w₁, w₂ и y, поэтому мы запишем это решение как c(w₁, w₂, yH)Ошибка! Не указан аргумент ключа.. Эта функция известна как функция издержек, и она будет представлять для нас значительный интерес. Функция издержек c(w₁, w₂, yJ)Ошибка! Не указан аргумент ключа. показывает минимальные издержки производства y единиц выпуска при ценах факторов, равных (w₁, w₂Ошибка! Не указан аргумент ключа.).

Чтобы понять решение этой задачи, изобразим функцию издержек и технологические ограничения для фирмы на одном графике. Изокванты дают нам технологические ограничения — все комбинации x₁ и x₂Ошибка! Не указан аргумент ключа., с помощью которых можно произвести y.

Предположим, что мы хотим нанести на график все комбинации факторов, дающие один и тот же уровень издержек C. Мы можем записать это в виде выражения

 

w₁x₁ + w₂x₂ = C

 

которое может быть преобразовано в

 

x₂ = —x₁

 

Легко увидеть, что это уравнение прямой, имеющей наклон —w₁/w₂ и точку пересечения с вертикальной осью C/w₂. Изменяя число C, мы получаем целое семейство изокост. Каждая точка изокосты выражает одни и те же издержки C, и более высокие изокосты связаны с большими издержками.

Таким образом, наша задача минимизации издержек может быть перефразирована следующим образом: найти на изокванте точку, с которой связана самая низкая изокоста. Такая точка показана на рис.19.1.

Обратите внимание на то, что если оптимальное решение предполагает использование некоторого количества каждого из факторов и если изокванта представляет собой гладкую кривую, то точка минимизации издержек будет характеризоваться условием касания: наклон изокванты должен быть равен наклону изокосты. Или, пользуясь терминологией гл.17, технологическая норма замещения должна равняться отношению цен факторов:

 

                                               —= TRS(, ) = —.                                   (19.1)

 

(В случае краевого решения, когда один из двух факторов не используется, условие касания удовлетворяться не должно. Аналогичным образом, если производственная функция имеет "изломы", условие касания теряет смысл. Эти исключения подобны исключениям в ситуации с потребителем, поэтому в настоящей главе мы не будем акцентировать внимание на указанных случаях.)

 

 

Рис. 19.1

Минимизация издержек. Выбор количеств факторов, минимизирующих издержки производства, может определяться нахождением на изокванте точки, связываемой с самой низкой изокостой.

 

Алгебра, скрывающаяся за уравнением (19.1), трудностей не представляет. Рассмотрим любое изменение структуры производства (Dx₁, Dx₂S), при котором выпуск остается постоянным. Такое изменение должно удовлетворять уравнению:

 

                                              MP₁(, )Dx₁ + MP₂(, )Dx₂ = 0.                                  (19.2)

 

Обратите внимание на то, что Dx₁T и Dx₂U должны иметь противоположные знаки; если вы увеличиваете используемое количество фактора 1, то для сохранения выпуска неизменным вам придется уменьшить используемое количество фактора 2.

Если мы находимся в точке минимума издержек, то данное изменение не может привести к снижению издержек, поэтому должно соблюдаться условие:

 

                                                                  w₁Dx₁ + w₂Dx₂ ³ 0.                                                      (19.3)

Теперь рассмотрим изменение (—Dx₁, —Dx₂VW), при котором также производится постоянный объем выпуска и издержки также не могут снижаться. Это подразумевает, что

 

                                                               —w₁Dx₁ — w₂Dx₂ ³ 0.                                                   (19.4)

 

Сложив выражения (19.3) и (19.4), получим

 

                                                                  w₁Dx₁ + w₂Dx₂ = 0.                                                      (19.5)

 

Решение уравнений (19.2) и (19.5) для Dx₂/Dx₁X дает нам

 

= —= —,

 

а это не что иное, как условие минимизации издержек, выведенное выше путем геометрических рассуждений.

Обратите внимание на некоторое сходство рис. 19.1 с решением задачи потребительского выбора, графически изображенным ранее. Хотя эти решения и выглядят одинаково, на самом деле они относятся к разным задачам. В задаче потребительского выбора прямая являлась бюджетным ограничением, и потребитель в поисках наиболее предпочитаемого положения двигался вдоль бюджетного ограничения. В задаче с производителем изокванта представляет собой технологическое ограничение, и производитель в поисках оптимального положения перемещается вдоль изокванты.

Выбор количеств факторов, минимизирующих издержки фирмы, вообще говоря, зависит от цен факторов и от того объема выпуска, который фирма хочет производить, поэтому мы записываем эти выбранные количества факторов в виде x₁(w₁, w₂, yY)Z и x₂(w₁, w₂, yAA)BB. Это так называемые функции условного спроса на факторы, или функции производного спроса на факторы. Они показывают взаимосвязь между ценами и выпуском и оптимальный выбор фирмой количества факторов при условии производства фирмой заданного объема выпуска y.

Обратите особое внимание на различие между функциями условного спроса на факторы и функциями спроса на факторы, максимизирующего прибыль, которые были рассмотрены в предыдущей главе. Функции условного спроса на факторы показывают выбор, минимизирующий издержки при заданном объеме выпуска; функции же спроса на факторы, максимизирующего прибыль, показывают выбор, максимизирующий прибыль при заданной цене фактора.

Функции условного спроса на факторы, как правило, не являются непосредственно наблюдаемыми: они представляют собой гипотетическое построение и отвечают на вопрос, сколько каждого фактора использовала бы фирма, если бы хотела произвести заданный объем выпуска самым дешевым способом. Однако функции условного спроса на факторы полезны в качестве способа отделения задачи определения оптимального объема выпуска от задачи определения метода производства, минимизирующего издержки.

17.Взаимосвязь между краткосрочными и долгосрочными издержками.

В проведенном выше анализе мы рассматривали в качестве постоянных издержек фирмы издержки, связанные с оплатой факторов, не подлежащих изменению в краткосрочном периоде. В длительном периоде фирма может выбирать количество используемых ею "постоянных" факторов — они более уже не являются постоянными.

Разумеется, в длительном периоде по-прежнему могут иметься квазипостоянные факторы. Иными словами, данная технология может обладать тем свойством, что некоторые издержки придется оплачивать, чтобы произвести любой положительный объем выпуска. Однако в длительном периоде не существует постоянных издержек в том смысле, что всегда есть возможность произвести ноль единиц выпуска при нулевых издержках, иными словами, всегда существует возможность прекратить деятельность. Если в длительном периоде имеются квазипостоянные факторы, то кривая средних издержек будет иметь, как и в коротком периоде, U-образную форму. Но в длительном периоде, по самому его определению, всегда будет существовать возможность производства нулевого выпуска при нулевых издержках. Конечно, какой именно период следует считать длительным, зависит от исследуемой задачи. Если в качестве постоянного фактора мы рассматриваем размеры завода (здесь и далее под размером завода понимаются производственные мощности), то продолжительность длительного периода будет определяться тем, сколько времени потребуется фирме, чтобы изменить размеры своего завода. Если мы рассматриваем в качестве постоянного фактора контрактные обязательства по выплате заработной платы, то продолжительность длительного периода будет зависеть от того, сколько времени потребуется фирме, чтобы изменить количество используемой ею рабочей силы. Чтобы быть конкретнее, будем считать постоянным фактором размер завода и обозначим его размер буквой k. Функцию краткосрочных издержек фирмы при условии, что фирма имеет завод площадью k квадратных футов, обозначим через c_s(y, k), где нижний индекс s обозначает "краткосрочный период" (k здесь играет такую же роль, какую в гл. 19 играет ). Для любого данного объема выпуска всегда существует какой-то размер завода, который оптимален для производства этого объема выпуска. Обозначим этот размер завода через k(y). Это условный спрос фирмы на фактор (в роли которого выступает размер завода) как функция выпуска. (Разумеется, он также зависит от цены размера завода и от цен других факторов производства, но эти аспекты аргументации мы оставляем в стороне). Тогда, как мы видели в гл. 19, функция долгосрочных издержек фирмы будет задана выражением c_s(y, k(y)). Это общие издержки производства объема выпуска y при условии, что фирма имеет возможность оптимально изменять размеры своего завода. Функция долгосрочных издержек фирмы есть не что иное, как функция ее краткосрочных издержек, оцененная в точке оптимального выбора постоянных факторов:

c(y) = c_s(y, k(y)).

Посмотрим, как это выглядит на графике. Выберем какой-то объем выпуска y* и обозначим через k* = k(y*) оптимальный размер завода для данного объема выпуска. Функция краткосрочных издержек для завода размером k* задается выражением c_s(y, k*), а функция долгосрочных издержек — выражением c(y) = c_s(y, k(y)), как показано выше. Теперь обратите внимание на тот важный факт, что краткосрочные издержки производства выпуска y должны всегда быть по крайней мере не меньше, чем долгосрочные издержки производства y. Почему? В краткосрочном периоде размер завода фирмы постоянен, в то время как в долгосрочном периоде фирма вольна изменять размер своего завода. Поскольку одним из возможных вариантов выбора фирмы в длительном периоде является выбор завода размером k*, оптимальному выбору производства y единиц выпуска должны соответствовать издержки по крайней мере не большие, чем c(y, k*). Это означает, что при изменении размера завода дела фирмы должны идти по крайней мере не хуже, чем при постоянном размере завода. Поэтому           

c(y) £ c_s(y, k*)

 для всех объемов выпуска y.

На самом деле мы знаем, что для одного конкретного объема y, а именно для y*,

c(y*) = c_s(y*, k*).

Почему это так? Потому что при y* оптимальным выбором размера завода является k*. Поэтому при y* долгосрочные и краткосрочные издержки производства оказываются одинаковыми.

Если краткосрочные издержки всегда больше долгосрочных и они равны при равном объеме выпуска, это означает, что краткосрочные и долгосрочные издержки обладают одним и тем же свойством: AC(y) £ AC_s(y, k*) и AC(y*) = AC_s(y*, k*). Это подразумевает, что кривая краткосрочных средних издержек всегда лежит над кривой долгосрочных средних издержек и они касаются друг друга в одной точке y*. Поэтому кривая долгосрочных средних издержек (LAC) и кривая краткосрочных средних издержек (SAC) в этой точке должны касаться друг друга, как показано на рис.20.6.

 

Краткосрочные и долгосрочные средние издержки. Кривая краткосрочных средних издержек должна касаться кривой долгосрочных средних издержек.

Рис. 20.6

Мы можем проделать такого же рода построения для объемов выпуска, отличных от y*. Предположим, что мы выбираем объемы выпуска y₁, y₂, ..., y_n и соответствующие им размеры завода k₁ = k(y₁), k₂ = k(y₂), ..., k_n = k(y_n). Тогда получаем картину, подобную изображенной на рис.20.7. Суть рис.20.7 заключается в утверждении, что кривая долгосрочных средних издержек огибает кривые краткосрочных средних издержек снизу.

Допустим, например, что имеются четыре различных варианта выбора размера завода, k₁, k₂, k₃ и k₄. На рис.20.8 изображены четыре различные кривые средних издержек, соответствующих этим размерам завода.

Рисунок 20.8 Дискретные уровни размера завода

Как можно построить кривую долгосрочных издержек? Вспомним, что кривая долгосрочных средних издержек есть та кривая издержек, которую мы получаем, оптимально изменяя k. В данном случае сделать это нетрудно: поскольку у нас всего четыре различных размера завода, мы просто смотрим, какому из них соответствуют наименьшие издержки, и выбираем именно этот размер завода. Иными словами, для любого объема выпуска y мы просто выбираем такой размер завода, который дает минимальные издержки производства данного объема выпуска.

Таким образом, кривая долгосрочных средних издержек должна, как показано на рис.20.8, являться нижней огибающей кривых краткосрочных средних издержек. Обратите внимание на то, что качественный смысл этого рисунка тот же самый, что и рис.20.7: краткосрочные средние издержки всегда по крайней мере не меньше долгосрочных средних издержек, и указанные издержки равны при том объеме выпуска, при котором долгосрочный спрос на постоянный фактор равен имеющемуся у вас количеству постоянного фактора.

Как мы видели в предыдущем параграфе, кривая долгосрочных средних издержек есть нижняя огибающая кривых краткосрочных средних издержек. Что из этого следует применительно к предельным издержкам? Вначале рассмотрим случай с дискретными размерами завода. В этой ситуации кривая долгосрочных предельных издержек состоит, как показано на рис.20.9, из соответствующих кусков кривых краткосрочных предельных издержек. При каждом объеме выпуска мы смотрим, в соответствии с какой кривой краткосрочных средних издержек мы производим, а затем на то, какие предельные издержки связываются с данной кривой.

Это должно быть верно независимо от того, сколько у нас имеется различных размеров завода, так что в случае их непрерывного количества получаем картину, подобную изображенной на рис.20.10. Долгосрочные предельные издержки при любом объеме выпуска y должны равняться краткосрочным предельным издержкам, связанным с размером завода, оптимальным для производства выпуска y.

 

 

Применим факты, выясненные нами в отношении кривых издержек, для того чтобы вычислить кривую предложения конкурентной фирмы. По определению, конкурентная фирма игнорирует свое влияние на рыночную цену. Таким образом, задачу максимизации, стоящую перед конкурентной фирмой, можно записать:

max py — c(y).

Это говорит просто о том, что конкурентная фирма хочет максимизировать свою прибыль: разность между общим доходом py и издержками c(y).

Какой объем выпуска решит производить конкурентная фирма? Ответ: она будет действовать в точке, где предельный доход равен предельным издержкам, — там, где добавочный доход, приносимый еще одной единицей выпуска, как раз равен добавочным издержкам производства еще одной единицы выпуска. Если бы данное условие не удовлетворялось, фирма всегда могла бы увеличить свою прибыль путем изменения своего объема выпуска.

В случае конкурентной фирмы предельный доход есть просто цена. Чтобы увидеть это, спросим себя, сколько добавочного дохода получит конкурентная фирма, увеличив выпуск на Dy. Мы получим

DR = pDy,

поскольку согласно нашей гипотезе p не изменяется. Поэтому добавочный доход на единицу выпуска задается формулой

DR/Dy = p,

представляющей собой выражение для предельного дохода.

Таким образом, конкурентная фирма выберет объем выпуска y в точке, где предельные издержки как раз равны рыночной цене. В условных обозначениях:

p = MC(y).

Мы хотим найти объем выпуска, максимизирующий прибыль при данной рыночной цене p. Если при каком-то объеме выпуска y цена больше предельных издержек, фирма может увеличить свою прибыль, чуть увеличив выпуск. Ведь превышение ценой предельных издержек означает, что

p — .

Поэтому увеличение выпуска на Dy означает, что

 

pDy — .

Упростив это неравенство, мы находим, что

pDy —Dc > 0,

а это означает, что прирост общего дохода от добавочного выпуска превышает прирост издержек. Следовательно, прибыль при этом должна увеличиться.

Аналогичные рассуждения можно провести и для случая, когда цена ниже предельных издержек. Тогда сокращение выпуска приведет к увеличению прибыли, поскольку потерянный при этом доход более, чем компенсируется сократившимися издержками.

Таким образом, при оптимальном объеме выпуска фирма должна производить в точке, где цена равна предельным издержкам. Каков бы ни был уровень рыночной цены p, фирма выберет объем выпуска y, соответствующий условию p = MC(y). Поэтому кривая предельных издержек конкурентной фирмы есть в точности ее кривая предложения. Или, другими словами, рыночная цена есть в точности предельные издержки до тех пор, пока каждая фирма производит объем выпуска, максимизирующий ее прибыль.

Рисунок 21.2 Предельные издержки и предложение.

В данных рассуждениях предполагается, что выгодно производить что-то. Но в конце концов самым выгодным для фирмы могло бы оказаться и производство нулевого выпуска. Поскольку всегда имеется возможность произвести нулевой объем выпуска, мы должны сравнить точку предполагаемой максимизации прибыли с точкой нулевого производства.

Если фирма производит нулевой выпуск, она по-прежнему должна оплачивать постоянные издержки F. Следовательно, прибыль от производства нуля единиц выпуска равна просто —F. Прибыль от производства объема выпуска y есть py — c_v(y) — F. Фирме выгоднее прекратить деятельность, когда

—F > py —c_v(y) —F,

т.е. когда "прибыль" от нулевого производства и просто оплаты постоянных издержек превышает прибыль от производства в точке, где цена равна предельным издержкам. Преобразование этого неравенства дает нам условие закрытия:

 Если средние переменные издержки больше p, фирме выгоднее производить ноль единиц выпуска. В этом есть смысл, поскольку это условие говорит о том, что общий доход от продажи выпуска y не покрывает даже переменных издержек производства c_v(y). В этом случае фирме лучше выйти из бизнеса. Если она не будет производить ничего, она потеряет постоянные издержки, но она потеряла бы даже больше, если бы продолжала производить.

Эти рассуждения показывают, что только те части кривой предельных издержек, которые лежат над кривой средних переменных издержек, могут состоять из точек, принадлежащих кривой предложения. Если точка, в которой цена равна предельным издержкам, находится под кривой средних переменных издержек, то в оптимуме фирма предпочтет производить нуль единиц выпуска.

Теперь перед нами вырисовывается картина кривой предложения, подобная изображенной на рис.21.3. Конкурентная фирма производит в той части кривой предельных издержек, которая является восходящей и лежит над кривой средних переменных издержек.

Рисунок 21.3 Средние переменные издержки и предложение.

Кривая долгосрочного предложения конкурентной фирмы строится на основании тех же принципов, что и кривая ее краткосрочного предложения. Поскольку по условию оптимальности P=MC , кривая предложения в долгосрочном периоде совпадает с кривой долгосрочных предельных издержек. Но в долгосрочном периоде все издержки фирмы являются переменными. Если цена становится ниже минимальных средних издержек, то фирма может избавиться от убытков, просто прекратив выпуск. Поэтому кривая долгосрочного предложения фирмы совпадает с кривой долгосрочных предельных издержек только на участке, лежащем не ниже минимума средних издержек, при P>=minAC. Квазипостоянные издержки — это издержки, которые тоже не зависят от объема выпуска, но должны оплачиваться только при условии производства фирмой положительного объема выпуска.

В длительном периоде по определению постоянных издержек не бывает, однако вполне могут существовать квазипостоянные издержки. Если началу производства какого-то объема выпуска должна предшествовать затрата какой-то постоянной суммы, то можно говорить о наличии квазипостоянных издержек.

18.Влияние налогов и субсидий на краткосрочное и долгосрочное равновесие конкурентной фирмы и отрасли, благосостояние и эффективность

Пусть монополисту установлена максимальная цена P. По цене выше установленной монополист продавать продукцию не может, значит он теряет часть кривой спроса, выше точки (Q,P). В области действия максимальной цены, т.е. значений выпуска меньше Q (dP/dQ)=0 (это вытекает из равенства

P+Q)  и поэтому MR(Q)=P

При выпуске больше Q (dP/dQ)<0 и потому MR(Q)<P. При выпуске, равном Q, кривая MR имеет разрыв и предельная выручка не определена.

 Если кривая SMC монополиста проходит через разрыв, то оптимальным для монополиста является выпуск, соответствующий установленной цене. При меньшем выпуске MR располагается выше MC, поэтому монополисту емеет смысл увеличить выпуск до Q; при большем выпуске MR ниже MC, и имеет смысл снизить выпуск до Q. Таким образом, с введением "потолка" цены для монополиста его выпуск растет по сравнению с тем выпуском, который он производил бы в отсутствие регулирования.

Рассмотрим фирму с постоянными предельными издержками и зададим вопрос, что произойдет с назначаемой ценой при введении потоварного налога. Ясно, что предельные издержки возрастут на сумму налога, но что произойдет с рыночной ценой? Сначала рассмотрим случай линейной кривой спроса, представленный на рис.23.3. Когда кривая предельных издержек MC сдвигается вверх на величину налога до кривой MC + t, точка пересечения кривой предельного дохода и кривой предельных издержек сдвигается влево. Поскольку кривая спроса имеет наклон вдвое меньший, чем кривая предельного дохода, цена возрастает на половину суммы налога. Это легко увидеть с помощью алгебраической записи. Условие равенства предельного дохода предельным издержкам плюс налог есть

a — 2by=c + t.

Решив это уравнение для y, получаем

.

Рисунок 23.2 Монополия с постоянной эластичностью спроса.

Следовательно, изменение выпуска задается формулой

= —.

Кривая спроса есть   p(y) = a — by, поэтому изменение цены будет равно (-b), умноженному на изменение объема выпуска:

 = —b ´ —.

В этом расчете дробь 1/2 появляется вследствие предпосылок о линейности кривой спроса и постоянных предельных издержках. Взятые вместе, эти предпосылки подразумевают, что цена возрастает на величину меньшую, чем налог. Может ли дело обстоять так в общем случае?

На этот вопрос следует ответить "нет": в общем случае налог может увеличивать цену на величину большую или меньшую, чем сумма налога. В качестве простого примера рассмотрим случай монополиста, сталкивающегося с кривой спроса постоянной эластичности. Тогда мы имеем

                                                         p =  

так что

                                                           ,

что, конечно, больше 1. В этом случае монополист перекладывает на покупателей сумму большую, чем налог.

Рисунок 23.3 Линейная кривая спроса и налогооблажение.

Можно было бы рассмотреть налог другого рода — налог на прибыль. В этом случае монополист должен выплачивать правительству какую-то долю LL своей прибыли. Задача максимизации прибыли, с которой сталкивается монополист, тогда принимает вид

max (1 — t) [p(y)y — c(y)].

Однако то значение y, которое максимизирует прибыль, будет максимизировать также величину (1 — t), умноженную на прибыль. Следовательно, чистый налог на прибыль не окажет воздействия на выбор объема выпуска монополистом.

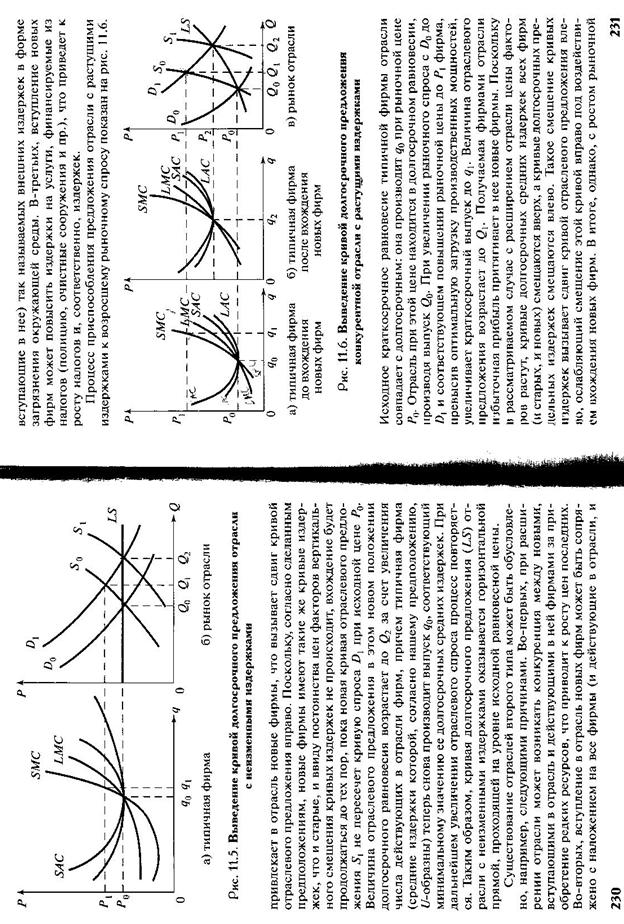
19. Долгосрочное предложение конкурентных отраслей с неизменными, растущими убывающими издержками.