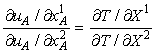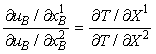49. Приведенная стоимость
потоков платежей. Определение цены бессрочной облигации.
|
|
§ 3. Современная стоимость потока
платежей
Станислав Агапов
В предыдущем параграфе мы говорили о нахождении
приведённой стоимости произвольной датированной суммы денег. Мы отметили, что
два или более платежа, приведённые к одному и тому же моменту времени, могут
не только напрямую сравниваться между собой, но и суммироваться. Последнее свойство
называется принципом слагаемости стоимостей.
|
|
Пример
|
Поясним принцип слагаемости стоимостей на простом
примере. Допустим, что некие надёжные люди предлагают вам вложить в их
предприятие 40 тысяч евро и гарантируют, что в качестве компенсации выплатят
вам в конце первого и второго годов по 30 тысяч евро. Таким образом, денежный
поток данной финансовой операции задаётся следующей таблицей:
|
Год
|
Платёж, евро
|
|
0
|
–
40 000
|
|
1
|
30
000
|
|
2
|
30
000
|
Допустим, что лучший из доступных вам альтернативных
способов размещения средств — это вложить их под 25% годовых. Как
определить, стоит ли вам принимать участие в предлагаемом проекте или нет?
Чтобы ответить на этот вопрос, вы можете рассуждать
следующим образом. Чтобы получить через год 30 тысяч евро, сегодня вам нужно
вложить 30 · (1 + 0,25)–1 = 24
тысячи евро под 25% годовых. Аналогично, чтобы получить 30 тысяч евро через
два года, сегодня вам нужно вложить 30 · (1 + 0,25)–2 = 19,2
тысячи евро. Сумма этих вложений составляет 43,2 тысячи евро, что на 3,2
тысячи больше, чем имеющаяся у вас на руках сумма. Значит, ваш альтернативный
способ вложения денег по сравнению с предлагаемым проектом требует
бóльших начальных вложений при том же будущем доходе. То есть
он хуже.
В основе этого рассуждения, очевидно, лежит операция сложения
дисконтированных значений платежей. То есть сначала мы нашли дисконтированное
значение вашего первого денежного поступления (получилось 24 тысячи евро),
затем второго (19,2 тысячи), а затем мы их сложили и получили результат, на
3,2 тысячи превосходящий имеющиеся у вас в начальный момент денежные
средства. То есть сравнили сумму дисконтированных значений ваших поступлений
и ваши начальные вложения, и на основании этого сравнения сделали наш вывод.
|
|
|
Дисконтирование потока платежей
Как видно из примера, принцип слагаемости стоимостей
позволяет определять приведённую стоимость целого денежного потока как сумму
приведённых стоимостей его платежей. Как мы увидим далее, в практических
расчётах обычно вычисляется приведённая стоимость потоков платежей на
начальный момент времени, которая называется современной стоимостью
потока.
Формализуем это понятие. Пусть A = {Ak; tk}
— это произвольный денежный поток. Допустим, что также задана некоторая
сложная годовая процентная ставка i, которая называется ставкой
дисконтирования. Тогда современной стоимостью потока платежей A
относительно данной процентной ставки называется число
|
|
(3.1)
|
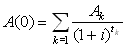 . .
|
|
|
Современную стоимость потока платежей также часто
называют его приведённой стоимостью (опуская упоминание о том, что
платежи приводятся именно к начальному моменту времени).
Каждое слагаемое в правой части формулы (3.1) — это
современное (дисконтированное) значение будущего платежа Ak.
Действительно, если вложить сумму денег
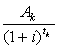
под сложную процентную ставку i на период
времени tk, то по его окончании сумма вклада составит
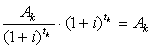 . .
Как вы помните, нахождение текущей стоимости будущего
значения капитала называется дисконтированием. Значит, формулу (3.1)
можно описать таким образом: современная стоимость денежного потока равна
сумме дисконтированных значений его платежей.
|
|
Пример
|
Напомню, что эффективная процентная ставка — это
сложная процентная ставка по кредиту, рассчитанная в предположении, что все
платежи, необходимые для получения данного кредита, идут на его погашение.
Таким образом, современная стоимость потока выплат по кредиту (включая
первоначальную комиссию), вычисленная с использованием его эффективной
процентной ставки, в точности равна сумме кредита, а современная стоимость
всего потока (с учётом всех как положительных, так и отрицательных платежей)
равна нулю. Этот пример иллюстрирует принцип, согласно которому современная
стоимость потока платежей по финансовому договору, который добровольно
подписали две стороны, всегда равна нулю. Ведь в противном случае одна из
сторон окажется в проигрыше и не станет подписывать такой договор. Тут,
правда, есть одна тонкость, касающаяся ставки дисконтирования.
Предполагается, что обе стороны действуют максимально эффективно, то есть для
заёмщика эффективная ставка по данному договору является минимальной из всех
возможных, а для кредитора — максимальной (при прочих равных условиях).
Иначе такой договор просто не был бы подписан (так как минимум для одной
стороны его условия не являлись бы оптимальными).
|
Бессрочные
облигации — облигации без фиксированного срока
погашения. Например, в
Великобритании
Undated gilts (термин gilts применяется для долгосрочных и среднесрочных
государственных облигаций) представлены: 2,5%-ми консолями 1888 г.; 3,5%-ми
военными облигациями, погашаемыми после 1952 г.; 4%-ми
консолями. Под погашением понимается право правительства
погасить облигацию, но так как рыночный курс ниже номинала, то нет смысла
производить погашение.
Текущая
цена бессрочной облигации определяется из отношения ежегодного дохода к
рыночной
ставке процента (требуемой доходности по облигационному выпуску):
P=(С/r)
Данная
формула получена из общей формулы оценки актива: Р
= всех поступлений от
актива.
В данном случае поступления предполагаются на
неограниченном временном
промежутке:
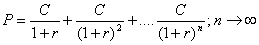
Умножив
обе части уравнения на (1+r)
и вычтя одно уравнение из другого, получим
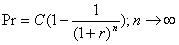 следовательно Pr = C
следовательно Pr = C
50. Чистая приведенная
стоимость как критерий в принятии инвестиционных решений. Внутренняя норма
окупаемости инвестиций.
Чистая современная ценность инвестиций
(NPV)
Синонимы: Чистая
текущая стоимость проекта. Чистый дисконтированный доход. Интегральный эффект
инвестиций. Чистая приведенная стоимость проекта.
Английские эквиваленты: Net present value (NPV). Net present worth
(NPW).
Показатель чистой современной ценности входит в число
наиболее часто используемых критериев эффективности инвестиций.
В общем случае методика расчета NPV заключается в
суммировании современных (пересчитанных на текущий момент) величин чистых эффективных
денежных потоков по всем интервалам планирования на всем протяжении периода
исследования. При этом, как правило, учитывается и ликвидационная или
остаточная стоимость проекта, формирующая дополнительный денежный поток за
пределами горизонта исследования. Для пересчета всех указанных величин
используются коэффициенты приведения, основанные на выбранной ставке сравнения
(дисконтирования).
Классическая формула
для расчета NPV выглядит следующим образом:
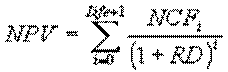 ,
,
где NCFi - чистый эффективный денежный поток на i-ом
интервале планирования, RD - ставка дисконтирования (в десятичном
выражении), Life - горизонт исследования, выраженный в интервалах
планирования.
Интерпретация расчетной величины чистой современной
стоимости может быть различной, в зависимости от целей инвестиционного анализа
и характера ставки дисконтирования. В простейшем случае NPV характеризует
абсолютную величину суммарного эффекта, достигаемого при осуществлении проекта,
пересчитанного на момент принятия решения при условии, что ставка дисконтирования
отражает стоимость капитала. Таким образом, в случае положительного значения
NPV рассматриваемый проект может быть признан как привлекательный с
инвестиционной точки зрения, нулевое значение соответствует равновесному
состоянию, а отрицательная величина NPV свидетельствует о невыгодности проекта
для потенциальных инвесторов.
Из макроэкономики –
чистая приведенная стоимость - сальдо от поступлений инвестиционного проекта и
дисконтированной стоимостью затрат на его осуществление.

IRR (внутренняя норма
доходности)
Внутренняя норма доходности (прибыли, внутренний коэффициент окупаемости,
Internal Rate of Return - IRR) - норма прибыли, порожденная инвестицией. Это та
норма прибыли (барьерная ставка, ставка дисконтирования),
при которой чистая текущая стоимость инвестиции равна нулю, или это та ставка
дисконта, при которой дисконтированные доходы от проекта равны инвестиционным
затратам. Внутренняя норма доходности определяет максимально приемлемую ставку
дисконта, при которой можно инвестировать средства без каких-либо потерь для
собственника.
IRR = r, при котором NPV = f(r) = 0,
Ее значение находят из следующего уравнения:
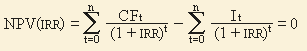
CFt - приток денежных средств в период t;
It - сумма инвестиций (затраты) в t-ом периоде;
n - суммарное число периодов (интервалов, шагов) t = 0, 1, 2, ..., n.
Экономический смысл данного
показателя заключается в том, что он показывает ожидаемую норму доходности
(рентабельность инвестиций) или максимально допустимый уровень инвестиционных
затрат в оцениваемый проект. IRR должен быть выше средневзвешенной цены
инвестиционных ресурсов:
IRR > CC.
Если это условие выдерживается, инвестор может принять проект, в противном
случае он должен быть отклонен.Достоинства показателя
внутренняя норма доходности (IRR) состоят в том, что кроме определения уровня
рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и
различной длительности.Показатель эффективности инвестиций внутренняя норма
доходности (IRR) имеет три основных недостатка.Во-первых, по умолчанию
предполагается, что положительные денежные потоки реинвестируются по ставке,
равной внутренней норме доходности. В случае, если IRR
близко к уровню реинвестиций фирмы, то этой проблемы не возникает; когда IRR,
особенно привлекательного инвестиционного проекта равен, к примеру 80%, то
имеется в виду, что все денежные поступления должны реинвестироваться при
ставке 80%. Однако маловероятно, что предприятие обладает ежегодными
инвестиционными возможностями, которые обеспечивают рентабельность в 80%. В данной
ситуации показатель внутренней нормы доходности (IRR) завышает эффект от
инвестиций (в показателе MIRR модифицированная внутренняя норма доходности
данная проблема устранена).Во-вторых, нет возможности
определить, сколько принесет денег инвестиция в абсолютных значениях (рублях,
долларах).В-третьих, в ситуации со знакопеременными
денежными потоками может рассчитываться несколько значений IRR или возможно
определение неправильного значения (в программе " Инвестиционный анализ
1.хх" эта проблема устранена программным способом).
Вопрос 51: Условия
достижения общего равновесия. Закон Вальраса.
Общим равновесием называется такое состояние, когда
наблюдается равновесие всех рыночных субъектов и на всех рынках. Математически
условие общего равновесия может быть записано так:
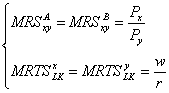
При этом первое равенство соответствует состоянию равновесия
в экономике обмена, а второе – в экономике производства. Более подробно о
состояниях равновесия в различных экономиках будет рассказано ниже, в ответах на
соответствующие вопросы.
Закон Вальраса
Закон Вальраса гласит, что если m-1 рынков находятся в состоянии
равновесия, то и оставшийся рынок также находится в равновесии, или
p1z1( p1, p2) + p2z2( p1, p2) º 0.
Иначе говоря, стоимость
совокупного избыточного спроса тождественно равна нулю. Утверждение
"стоимость совокупного спроса тождественно равна нулю" означает, что
она равна нулю для всех возможных выборов цен, а не только для равновесных цен.
Доказательство этого следует из
суммирования бюджетных ограничений двух индивидов. Рассмотрим вначале индивида
A. Поскольку его спрос на каждый товар удовлетворяет его бюджетному
ограничению, мы имеем
p1 (p1, p2) + p2
(p1, p2) + p2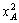 (p1,
p2) º p1
(p1,
p2) º p1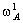 + p2
+ p2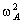
p1[ (p1,
p2) —
(p1,
p2) — 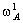 ]+ p2[
]+ p2[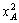 (p1,
p2) —
(p1,
p2) — 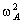 ] º 0
] º 0
p1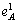 (p1, p2) + p2
(p1, p2) + p2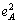 (p1,
p2) º 0.
(p1,
p2) º 0.
В этом уравнении утверждается,
что стоимость чистого спроса индивида A равна нулю. Иными словами, стоимость
того количества товара 1, которое хочет купить индивид A, плюс стоимость того
количества товара 2, которое он хочет купить, должна равняться нулю. (Конечно,
количество одного из товаров, которое он хочет купить, должно быть
отрицательным — иначе говоря, он намеревается продать один из товаров, чтобы
купить больше другого товара.)
У нас имеется аналогичное уравнение
для индивида B:
p1[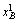 (p1, p2)
—
(p1, p2)
—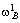 ]+ p2[
]+ p2[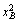 (p1, p2)
—
(p1, p2)
—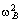 ] º 0,
] º 0,
p1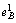 (p1, p2)
+ p2
(p1, p2)
+ p2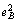 (p1, p2) º 0.
(p1, p2) º 0.
Сложив эти уравнения для
индивидов A и B и воспользовавшись определением совокупного спроса z1( p1, p2) и z2( p1, p2), получаем
p1[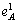 (p1, p2) +
(p1, p2) +  (p1, p2)] + p2[
(p1, p2)] + p2[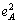 (p1, p2) +
(p1, p2) + 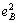 (p1, p2)] º 0,
(p1, p2)] º 0,
p1z1(p1,
p2) + p2z2(p1, p2) º 0.
Теперь можно увидеть, откуда
следует закон Вальраса: поскольку стоимость избыточного спроса каждого индивида
равна нулю, стоимость суммы избыточных спросов индивидов должна равняться нулю.
Теперь можно наглядно показать,
что при равенстве спроса предложению на одном рынке спрос должен быть равен
предложению и на другом рынке. Обратите внимание на то, что закон Вальраса
должен соблюдаться для всех цен, так как бюджетное ограничение каждого из
индивидов должно удовлетворяться при любых ценах. Поскольку закон Вальраса
соблюдается для всех цен, он, в частности, соблюдается для совокупности цен,
при которой избыточный спрос на товар 1 равен нулю:
z1(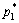 ,
, 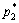 ) = 0.
) = 0.
Согласно закону Вальраса должно соблюдаться
p1z1(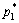 ,
, 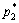 ) + p2z2(
) + p2z2(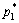 ,
,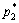 ) = 0.
) = 0.
Как легко вывести из этих уравнений, если p2
> 0, то должно быть
z2(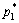 ,
,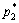 ) = 0.
) = 0.
Следовательно, как утверждалось
выше, если мы найдем совокупность цен (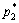 ,
,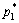 ), при
которой спрос на товар 1 равняется предложению товара 1, нам гарантировано, что
спрос на товар 2 должен равняться предложению товара 2. Напротив, если мы
найдем совокупность цен, при которой спрос на товар 2 равен предложению товара
2, нам гарантировано, что рынок товара 1 будет находиться в равновесии.
), при
которой спрос на товар 1 равняется предложению товара 1, нам гарантировано, что
спрос на товар 2 должен равняться предложению товара 2. Напротив, если мы
найдем совокупность цен, при которой спрос на товар 2 равен предложению товара
2, нам гарантировано, что рынок товара 1 будет находиться в равновесии.
Вообще, если имеются рынки для k товаров, достаточно найти
совокупность цен, при которой в равновесии пребывают k — 1 рынков. Из закона
Вальраса в этом случае будет следовать, что на рынке товара k спрос
автоматически должен быть равен предложению.
Вопрос 52: Общее равновесие
и эффективность в обмене. Кривая контрактов.
Обменная сделка
Проанализируем, как происходит обмен. Начнем с начального
запаса товаров, обозначенного на рис.28.1 точкой W.
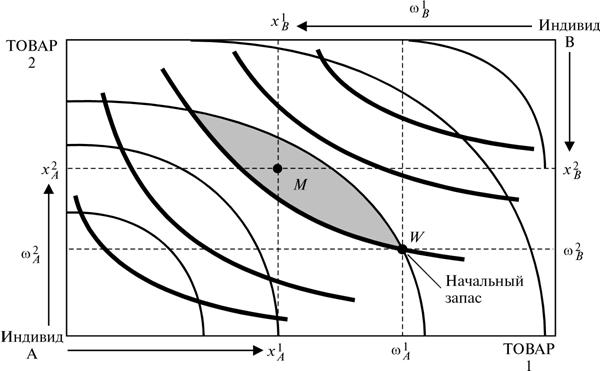
Рассмотрим кривые безразличия для
A и B, проходящие через это распределение. Область, в которой благосостояние A
выше, чем в точке его начального запаса, состоит из всех распределений,
находящихся над его кривой безразличия, проходящей через точку начального
запаса. Область, в которой благосостояние B выше, чем в точке его начального
запаса, состоит из всех распределений, находящихся, с точки зрения B, над его
кривой безразличия, проходящей через W. Где находится та область ящика, в
которой выше благосостояние и A, и B? Ясно, что она находится на пересечении
двух указанных областей. Это имеющая форму линзы область, показанная на
рис.28.1. Предположительно в ходе переговоров двум участвующим в них людям
удастся найти некую взаимовыгодную сделку, в результате которой они
передвинутся в какую-то точку внутри линзообразной области, подобную точке M на
рис.28.1.
Конкретное перемещение в точку M,
изображенное на рис.28.1, подразумевает отказ индивида A от | —
— 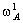 | единиц товара 1 и
приобретение в обмен |
| единиц товара 1 и
приобретение в обмен |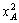 —
— 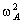 | единиц товара 2. Это
означает, что B приобретает |
| единиц товара 2. Это
означает, что B приобретает |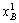 —
—  | товара 1 и отдает |
| товара 1 и отдает |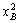 —
— 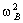 | единиц товара 2.
| единиц товара 2.
Теперь можно повторить тот же
самый анализ применительно к точке M. Мы можем провести через M две кривые
безразличия, построить новую линзообразную "область взаимной выгоды"
и представить себе, что участники сделки премещаются в какую-то новую точку N,
лежащую в этой области. Обмен будет продолжаться до тех пор, пока не
исчерпаются сделки, предпочитаемые обеими сторонами.
Распределения, эффективные по Парето
Ответ на этот вопрос дан
рис.28.2. В точке M данной диаграммы множество точек, располагающееся над
кривой безразличия индивида A, не пересекает множества точек, располагающегося
над кривой безразличия индивида B. Область, в которой благосостояние индивида A
становится выше, отделена от области, в которой становится выше благосостояние
индивида B. Это означает, что любое движение, повышающее благосостояние одной
из сторон, с необходимостью понижает благосостояние другой. Таким образом, не
существует обменных сделок, которые были бы выгодны для обеих сторон. При таком
распределении взаимовыгодные сделки отсутствуют.
Распределение такого рода
известно как распределение, эффективное по Парето. Распределение, эффективное
по Парето, можно описать как такое распределение, при котором:
- не существует способа повысить благосостояние всех
участвующих в обмене людей;
или
- не существует способа повысить благосостояние какого-либо
индивида без понижения благосостояния кого-то другого;
или
- все выгоды от обмена исчерпаны;
или
- отсутствует возможность совершения взаимовыгодных сделок и
т.д.
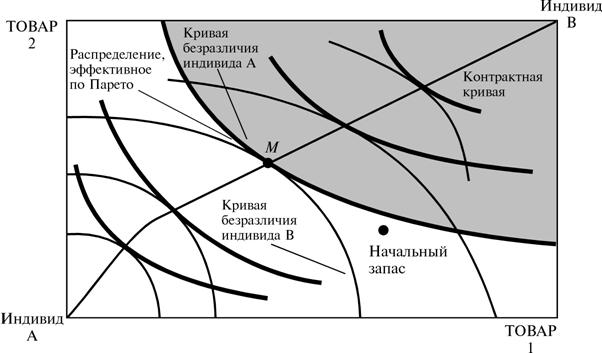
Рисунок 28.2
Распределение, эффективное по Парето.
Кривые безразличия двух
участников обмена при любом эффективном по Парето распределении в ящике
Эджуорта должны касаться друг друга. Почему это так, увидеть нетрудно. Если две
кривые безразличия не касаются друг друга в точке распределения внутри ящика
Эджуорта, значит, они должны пересекаться. Но если они пересекаются, то должна
существовать возможность совершения взаимовыгодной сделки — поэтому данная
точка не может быть эффективной по Парето. Из условия касания легко увидеть,
что в ящике Эджуорта существует много распределений, эффективных по Парето.
Фактически, если дана, например, любая кривая безразличия для индивида A,
существует простой способ найти распределение, эффективное по Парето. Просто
двигайтесь вдоль кривой безразличия для индивида A до тех пор, пока не найдете
точку, являющуюся наилучшей для индивида B. Это и будет точка распределения,
эффективного по Парето, и, следовательно, в ней обе кривые безразличия будут
касаться друг друга.
Множество всех точек
распределений, эффективных по Парето, в ящике Эджуорта называется множеством
Парето, или контрактной кривой. В типичном случае контрактная кривая проходит
от начала координат для A до начала координат для B через весь ящик Эджуорта,
как показано на рис.28.2. Начнем движение из начала координат для A: в этой
точке у индивида A нет ничего, все товары принадлежат индивиду B. Это
распределение эффективно по Парето, поскольку единственный способ, которым
можно повысить благосостояние A, состоит в том, чтобы отнять что-то у B. По
мере движения вверх по контрактной кривой благосостояние A все больше растет,
пока мы не доберемся, наконец, в начало координат для B.
Множество Парето описывает все
возможные исходы взаимовыгодного обмена, независимо от того, в какой точке
ящика мы начинаем движение. Если нам задана исходная точка, т.е. заданы
начальные запасы для каждого потребителя, можно рассмотреть такое подмножество
множества Парето, которое каждый из потребителей предпочтет своему начальному
запасу. Это просто то подмножество множества Парето,
которое лежит в линзообразной области, изображенной на рис.28.1. Распределения,
находящиеся в этой линзообразной области, являются возможными исходами
взаимного обмена, начинающегося с конкретного начального запаса,
представленного на этой диаграмме. Однако само множество Парето не зависит от
начального запаса, за исключением того обстоятельства, что начальный запас
определяет общие наличные количества обоих товаров и тем самым размеры ящика.
53-54.Общее равновесие и
эффективность в производстве. Кривая
производственных возможностей. Эффективность структуры выпуска.
Рассмотрим эффективные по Парето способы осуществления
выбора между технологически допустимыми потребительскими наборами.
Обозначим совокупные потребительские наборы через (X1, X2). Это означает, что в наличии
для потребления имеются X1 единиц товара 1 и X2 единиц товара 2. В экономике Зная общее количество каждого товара, можно нарисовать ящик
Эджуорта, как на рис.29.9.
При заданном (X1,
X2) множество потребительских
наборов, эффективных по Парето, будет множеством такого же рода, как и
множества, рассмотренные в предыдущей главе: как показано на рис.29.9, объемы
потребления, эффективные по Парето, будут лежать на множестве Парето — линии
взаимных касаний кривых безразличия. Это такие распределения, при которых
предельная норма замещения каждого потребителя — пропорция, согласно которой он
как раз готов совершить обмен — равна предельной норме замещения другого
потребителя.
Указанные распределения являются эффективными по Парето в
том, что касается решений о потреблении. Если люди могут просто обменять один
товар на другой, то множество Парето описывает множество наборов, исчерпывающее
выгоды от обмена. Однако в экономике, где имеет место не только обмен, но и
потребление, существует другой способ обменять один товар на другой, а именно:
произвести меньше одного товара и больше другого.

Рисунок 29.9 Производство и ящик Эджуорта.
Множество Парето описывает множество наборов, эффективных
по Парето, при заданных наличных количествах товаров 1 и 2, однако, в
экономике, где имеется производство, сами эти количества могут быть выбраны из
множества производственных возможностей. Какие варианты
выбора из множества производственных возможностей будут эффективными по Парето?
Представим себе логику, лежащую в основе условия,
связанного с предельной нормой замещения. Как нами утверждалось, в точке распределения,
эффективного по Парето, MRS потребителя A должна равняться MRS потребителя B:
пропорция, в которой потребитель A как раз хотел бы обменять один товар на
другой, должна быть равна пропорции, в которой потребитель B как раз готов
обменять один товар на другой. Если бы это было не так, то существовала бы
какая-то обменная сделка, в результате которой повысилось бы благосостояние
обоих потребителей.
Вспомним, что предельная норма трансформации (MRT)
измеряет пропорцию, в которой можно «превратить» один товар в другой. Конечно,
в действительности не происходит буквального превращения одного товара в
другой. Происходит, скорее, перемещение факторов производства с тем, чтобы
производить меньше одного товара и больше другого.
Предположим, что экономика функционирует в точке, где
предельная норма замещения у одного из потребителей не равна предельной норме
трансформации одного товара в другой. В таком случае указанная точка не может
быть эффективной по Парето. Почему? Потому что в этой точке пропорция, в которой
потребитель готов обменять товар 1 на товар 2, отличается от пропорции, в
которой товар 1 может быть превращен в товар 2 — существует способ повысить
благосостояние данного потребителя, изменив структуру производства.
Допустим, например, что MRS данного потребителя равна 1; потребитель готов заменить товар 2 товаром 1 в
пропорции один к одному. Допустим, что MRT равна 2;
это означает, что отказ от одной единицы товара 1 позволит обществу произвести
две единицы товара 2. Поскольку потребителю безразлично, отказаться от одной
единицы товара 1, получив взамен одну единицу другого товара, или нет, его
благосостояние, конечно, повысится, если он получит две добавочные единицы
товара 2.
Этот же довод можно привести всегда, когда у одного из
потребителей MRS отлична от MRT — в этом случае всегда
можно произвести перестройку потребления и производства, в результате которой
благосостояние данного потребителя повысится. Как мы уже видели, в ситуации,
эффективной по Парето, MRS каждого потребителя должна быть одной и той же, а из
приведенных выше рассуждений следует, что MRS каждого потребителя должна,
фактически, равняться MRT.
Рис.29.9 иллюстрирует распределение, эффективное по
Парето. MRS у всех потребителей одинаковы, так как их кривые безразличия в
ящике Эджуорта касаются друг друга. И MRS каждого потребителя равна MRT — наклону границы множества производственных
возможностей.
Алгебраическая формализация модели
Выведем условия эффективности по Парето в экономике, где
имеется не только обмен, но и производство, воспользовавшись дифференциальным
исчислением. Пусть X1 и X2 представляют,
как в основной части главы, общее произведенное и
потребленное количество товаров 1 и 2:
X1 = 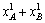
X2 = 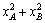 .
.
Первое, что нам требуется, — это найти удобный способ
описания границы производственных возможностей, т.е. всех технологически
допустимых комбинаций X1 и X2. Для наших целей удобнее
всего сделать это, воспользовавшись функцией трансформации. Это функция
совокупных количеств двух товаров T(X1, X2), таких, что комбинация
(X1, X2) находится на границе производственных
возможностей (границе множества производственных возможностей), если и только
если
T(X1, X2) =
0.
Описав технологию, можно вычислить предельную норму
трансформации — пропорцию, в которой мы должны пожертвовать товаром 2, чтобы
произвести больше товара 1. Хотя данное название и вызывает в представлении
картину «превращения» одного товара в другой, эта картина несколько обманчива.
На самом деле происходит перемещение ресурсов из производства товара 2 в
производство товара 1. Таким образом, уделяя меньше ресурсов производству
товара 2 и больше — производству товара 1, мы перемещаемся из одной точки на
границе производственных возможностей в другую. Предельная норма трансформации
есть не что иное, как наклон границы множества производственных возможностей,
обозначаемый нами как dX2/dX1.
Рассмотрим малое изменение производства
(dX1, dX2), остающееся практически
осуществимым. Мы получаем поэтому следующее уравнение:
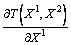 dX1 +
dX1 + 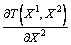 dX2
= 0.
dX2
= 0.
Найдя из него предельную норму трансформации, получаем
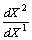 = —
= — .
.
В случае для двух индивидов можно записать указанную
задачу максимизации как
max uA( ,
,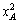 )
)

при uB (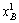 ,
,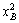 ) =
) = 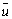
T(X1, X2) =
0.
Функция Лагранжа для данной задачи имеет вид
L = uA ( ,
,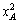 ) — l(uB (
) — l(uB (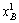 ,
,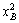 ) —
) — 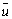 ) —
) —
— m(T(X1,
X2) — 0),
а условия первого порядка — вид
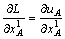 —
—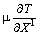 = 0,
= 0,
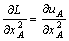 —
—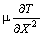 = 0
= 0
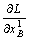 =
—
=
—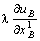 —
—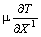 = 0
= 0
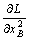 =
—
=
—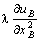 —
—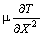 = 0.
= 0.
Выполнение преобразований и деление первого уравнения на
второе дает нам
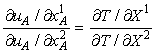 .
.
Выполнение той же самой операции над третьим и четвертым
уравнениями дает
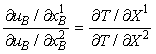 .
.
Левые части этих уравнений — предельные нормы замещения.
Правая часть этих уравнений — предельная норма трансформации. Таким образом,
указанные уравнения требуют, чтобы у каждого индивида предельная норма
замещения для двух товаров равнялась предельной норме трансформации: пропорция,
в которой каждый индивид готов заместить один товар другим, должна быть той же,
что и пропорция, в которой превращение одного товара в другой является
технологически допустимым. Предположим,
что MRS для какого-то индивида не равна MRT. Тогда
пропорция, в которой данный индивид был бы готов пожертвовать одним товаром
ради получения большего количества другого, отличалась бы от пропорции, в
которой превращение одного товара в другой является технологически допустимым —
но это означает, что существовал бы какой-то способ увеличения полезности для
данного индивида, не затрагивающий чьего-либо еще потребления.
КРИВАЯ ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ —
кривая, графически иллюстрирующая возможности одновременного производства двух
продуктов с учетом ограниченности ресурсов, расходуемых на производство этих
продуктов. Кривая строится в системе координат, каждая из которых отражает
объем производства одного из продуктов. Она ограничивает область
производственных возможностей, так что любая точка на кривой показывает
предельно возможное по ресурсным ограничениям сочетание объемов производства
двух продуктов.
Теорема Эрроу о невозможности
Теорема Эрроу о невозможности развивает
представления о несостоятельности общественного (коллективного) выбора. С
позиции Эрроу, функция общественного благосостояния - это не просто
определенные упорядоченные общественные предпочтения в отношении альтернативных
общественных состояний, а сам механизм (процедура) такого упорядочивания,
своего рода набор правил («конституция»).
Действительно, очевидно, что для перехода от
индивидуальных предпочтений к общественным требуется
какой-то механизм агрегирования первых во вторые. Естественным стремлением в
ответ на парадокс голосования является попытка сконструировать этот механизм
(функцию общественного благосостояния по Эрроу) таким образом, чтобы он
обеспечивал транзитивность общественных предпочтений. При этом Эрроу предложил
четыре минимальных и весьма умеренных требования, которым этот механизм должен
отвечать.
1. Неограниченная
область определения (unrestricted domain). Иногда этот принцип переводят на
русский как «универсальность». Его смысл заключается в том, что механизм
агрегирования индивидуальных предпочтений в общественные действует для любой
комбинации индивидуальных предпочтений. Так, например, если общество
представляют 3 индивида и 3 альтернативы (x, y, z), то в любом случае у нас
имеется 63 = 216 возможных вариантов сочетаний индивидуальных предпочтений. Для
любого из них существует функция общественного благосостояния как способ
трансформации индивидуальных предпочтений в
общественные. Говоря математическим языком, в общем случае такая функция имеет
неограниченную область определения (отсюда и название принципа).
2. Отсутствие диктатуры
(non-dictatorship). Диктатор определяется как некто, чей выбор между парами
альтернатив является решающим, т. е. определяющим общественный выбор независимо
от предпочтений других. Например, если для индивида 1 x предпочтительнее y и
если обществу, независимо от предпочтений индивидов 2 и 3, присуща такая же
система предпочтений, то индивид 1 - диктатор.
3. Принцип Парето
(Pareto prinсiple). Здесь этот принцип можно
сформулировать следующим образом: если каждый предпочитает x по отношению к y,
тогда x должен быть предпочтительнее y и для общества.
4. Независимость от не
относящихся к делу альтернатив (independence of irrelevant alternatives). Пусть
общество предпочитает альтернативу x альтернативе y. Затем предположим, что
некое индивидуальное упорядочивание предпочтений изменилось таким образом, что
оно оставляет неизменным предпочтения каждого индивида между x и y. Тогда
общественное предпочтение x по отношению к y должно сохраниться. Так, изменение
z в индивидуальных предпочтениях не должно само по себе изменить характер
общественного предпочтения между x и y (иначе говоря, z - посторонняя
альтернатива при выборе между x и y).
Эрроу показал, что не существует такой функции
общественного благосостояния, которая удовлетворяет всем четырем условиям и
которая одновременно способна обеспечить транзитивность общественных
предпочтений. Таким образом, любая попытка выработать набор правил, который
трансформирует индивидуальные предпочтения в
общественные и удовлетворяет этим четырем требованиям, невозможна
Вопрос 55: Первая и вторая
теоремы экономики благосостояния.
Первая теорема экономики благосостояния
Конкурентное равновесие является
эффективным по Парето. Остается ли этот результат в силе для экономики, в
которой имеет место не только обмен, но и производство? Оказывается, следует
ответить "да": если фирмы ведут себя как конкурентные фирмы,
максимизирующие прибыль, то конкурентное равновесие будет эффективным по
Парето.
В отношении этого результата
следует сделать обычные предостережения. Во-первых, он не имеет ничего общего с
распределением богатства. Максимизация прибыли гарантирует лишь эффективность,
но не справедливость! Во-вторых, этот результат имеет смысл только тогда, когда
конкурентное равновесие действительно существует. В частности, он теряет смысл
применительно к большим областям возрастающей отдачи от масштаба. В-третьих,
неявной предпосылкой данной теоремы является то, что выбор любой фирмы не
оказывает влияния на производственные возможности других фирм. Иными словами,
данная теорема исключает возможность внешних эффектов со стороны производства.
Аналогичным образом теорема требует, чтобы производственные решения фирм не
влияли непосредственно на потребительские возможности потребителей; иными
словами, внешние эффекты со стороны потребления также отсутствуют.
Вторая теорема экономики благосостояния
В случае экономики чистого обмена
при выпуклых предпочтениях потребителей любое распределение, эффективное по
Парето, может быть конкурентным равновесием. Применительно к экономике, в
которой имеет место не только обмен, но и производство, тот же самый результат
остается справедливым, но теперь мы требуем, чтобы выпуклыми были не только
предпочтения потребителей, но и производственные множества фирм. Как уже
отмечалось, это требование, по существу, исключает возможность возрастающей
отдачи от масштаба: если при равновесном объеме производства фирмы имеют
возрастающую отдачу от масштаба, то они захотят производить больший выпуск при
конкурентных ценах.
Однако
для случаев постоянной или убывающей отдачи от масштаба вторая теорема
экономики благосостояния совершенно справедлива. Благодаря использованию
конкурентных рынков можно достичь любого распределения, эффективного по Парето.
Разумеется, обычно для поддержания различных распределений, эффективных по
Парето, требуется перераспределить между потребителями начальные запасы. В
частности, приходится перераспределять как доход от начальных запасов труда,
так и акции фирмы. Как показано в предыдущей главе, с такого рода
перераспределением могут быть связаны значительные практические трудности.
Вопрос 56. Кривая возможных
полезностей. Альтернативные подходы к формированию функции общественного
благосостояния.
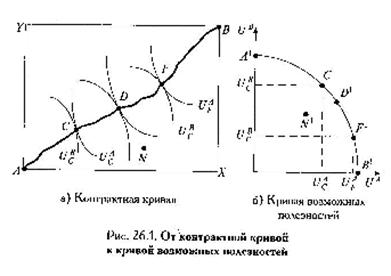
 Кривая возможных полезностей-изображение ящика Эджуорта
в координатах Ua, Ub, которая характеризует распределение полезностей между
субъектами Аи В. Пересечение кривой возможных полезностей с вертикальной
осью-точка, которая соответствует расределению благ, при котором все блага
достаются В (На конкрактной кривой это начало ккординат для субъекта А).
Пересечение с горизонтальной осью-точка, в которой все блага достаются А(На конкрактной кривой это начало ккординат для субъекта
В). Кривая возможных полезностей имеет отрицательный наклон, так как при
движении вдоль кривой контрактов в ящике Эджуорта из левого нижнего угла в
правый верхний, сопровождается ростом полезности, получаемой субъектом А, и снижением полезности у В. Тангенс угла наклона кривой
отражает Альтернативную стоимость полезности субъекта А. При движении по
контрактной кривой из начала координат А в В, количество благ у субъекта А
увеличивается, а у В уменьшается.Согласно закону
убывающей MU, прирост Ua должен уменьшатся, а уменьшение Ub должно
возрастать=> отношение (Δua/ΔUb) при движении вниз по кривой
возможных полезностей будет возрастать=> эта кривая является выпуклой к
началу координат. Тк каждая точка этой кривой отражает уровни полезности,
получаемой веми членами общества (наше состоит из двух индивидов Аи В), она
характеризует уровень общественного благосостояния и поэтому ее называют кривой
возможных благосостояний. Она характеризует все возможные уровни общественного
благосостояния при достижении Паретто-эффективности. Если точка находится под
кривой общественного благосостояния, это означает, что блага распределяются
неэффективно по Паретто и что за счет перераспределения благ можно увеличить
полезность для всех членов общества. Следовательно, Паретто-эффективное
состояние экономики является необходимым условием максимизации общественного
благосостояния.
Кривая возможных полезностей-изображение ящика Эджуорта
в координатах Ua, Ub, которая характеризует распределение полезностей между
субъектами Аи В. Пересечение кривой возможных полезностей с вертикальной
осью-точка, которая соответствует расределению благ, при котором все блага
достаются В (На конкрактной кривой это начало ккординат для субъекта А).
Пересечение с горизонтальной осью-точка, в которой все блага достаются А(На конкрактной кривой это начало ккординат для субъекта
В). Кривая возможных полезностей имеет отрицательный наклон, так как при
движении вдоль кривой контрактов в ящике Эджуорта из левого нижнего угла в
правый верхний, сопровождается ростом полезности, получаемой субъектом А, и снижением полезности у В. Тангенс угла наклона кривой
отражает Альтернативную стоимость полезности субъекта А. При движении по
контрактной кривой из начала координат А в В, количество благ у субъекта А
увеличивается, а у В уменьшается.Согласно закону
убывающей MU, прирост Ua должен уменьшатся, а уменьшение Ub должно
возрастать=> отношение (Δua/ΔUb) при движении вниз по кривой
возможных полезностей будет возрастать=> эта кривая является выпуклой к
началу координат. Тк каждая точка этой кривой отражает уровни полезности,
получаемой веми членами общества (наше состоит из двух индивидов Аи В), она
характеризует уровень общественного благосостояния и поэтому ее называют кривой
возможных благосостояний. Она характеризует все возможные уровни общественного
благосостояния при достижении Паретто-эффективности. Если точка находится под
кривой общественного благосостояния, это означает, что блага распределяются
неэффективно по Паретто и что за счет перераспределения благ можно увеличить
полезность для всех членов общества. Следовательно, Паретто-эффективное
состояние экономики является необходимым условием максимизации общественного
благосостояния.
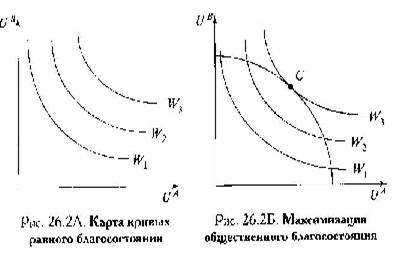
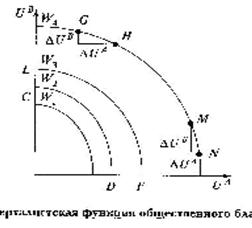 Функция
общественного благосостояния представляет собой функцию, зависящую от
благосостояния отдельных членов
общества. W=W(U1,U2,...,Ui,...Un). Кривые равного благосостояния расположенные
дальше от начала координат имеют более высокие уровни общественного
благосостояния. Если соединить карту кривых равного
благосостояний с кривой возможных полезностей, то станет очевидно, что
максимальный уровень обществнного благосостояния находится в точке их касания
=> максимум общественного благосостояния мб достигнут только при
Паретто-эффективном состоянии экономики, но не каждое Паретто-эффективное
распределение благ дает максимум общественного благосостояния и
Паретто-эффективность не является достаточным условием максимизации
общественной полезности. Необходимое условие-справедливое
распределение благосостояния с общественной точки зрения. Сущ-ют три
основных подхода к решению этого
вопроса:
Функция
общественного благосостояния представляет собой функцию, зависящую от
благосостояния отдельных членов
общества. W=W(U1,U2,...,Ui,...Un). Кривые равного благосостояния расположенные
дальше от начала координат имеют более высокие уровни общественного
благосостояния. Если соединить карту кривых равного
благосостояний с кривой возможных полезностей, то станет очевидно, что
максимальный уровень обществнного благосостояния находится в точке их касания
=> максимум общественного благосостояния мб достигнут только при
Паретто-эффективном состоянии экономики, но не каждое Паретто-эффективное
распределение благ дает максимум общественного благосостояния и
Паретто-эффективность не является достаточным условием максимизации
общественной полезности. Необходимое условие-справедливое
распределение благосостояния с общественной точки зрения. Сущ-ют три
основных подхода к решению этого
вопроса:
1. Либералистский подход. Распределение благ,
обеспечивающееся механизмом конкурентного рынка есть наиболее
справедливое (тк механизм конкурентного рынка обеспечивает эффективное
использование ресурсов). Также, с т.зр. Нозика, рыночное распределение является ненасильственным процессом => обмен справедлив =>
уонечное результаты будут являться справедливыми =>
Паретто-эффективное распределение благ обеспечивает максимум благосостояния. Следовательно функция общественного благосостояния мб
представлена в виде семейства кривых, совпадающих с кривыми возможных
полезностей.
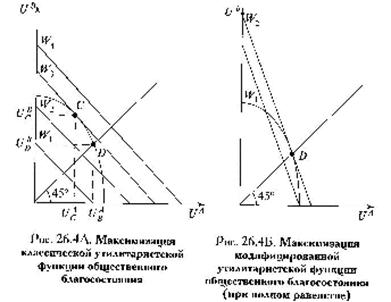 2. Утилитаристский подход.
2. Утилитаристский подход.
Общее
благосостояние есть арифметическая сумма благосостояния отдельных лиц:
W(U1,U2,...,Ui,...Un)=ΣUi. В двухсубъектной модели общества функция
принимает вид: W=Ua+Ub=> это карта линейных кривых равного благосостояния, c
tgα=1. Максимум общественного благосостояния достигается в точке касания кривых, но такое
распределение не является равным. Полное равнство
достигалось бы на луче равного распределения (биссектриса данного угла). Т.о.
Классическая утилитаристская функция может достигнуть максимального
благосостояния при абсолютном равенстве в распределении, если tg угла наклона кривой возможных полезностей
становится равным единице в точке пересечения с лучом равного распределения. В
утилитаристкой функции полезности MRS благосостояния индивида =1
=>полезность , получаемая каждым индивидом
равнозначна и равновеликий рост полености у бедных и богатых в раной степени
способствует росту общественного благосостояния.
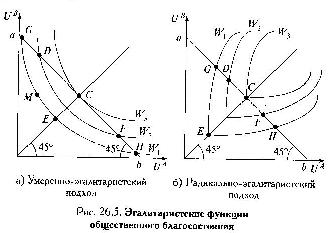 В
рамках данного подхода можно акцентировать внимание на уменьшении степени
общественного неравнства: W(U1,U2,...,Ui,...Un)=ΣKiUi, где Кi-характеризует значимость, которую общество придает
полезности отдельных индивидов. Если увеличить К для малообеспеченных членов
общества, неравенство в распределении благ уменьшится.
=> можно подобрать значения коэффициентов т.о.,
чтобы добиться максимума общественного благосостояния при абсолютно равном
распределении полезностей. Для
двухсубъектной модели общества функция принимает вид: W=КаUa+КbUb. Необходимо подобрать значение Ka/Kb=tgα, где α-угол наклона кривой возможных полезностей, в точке,
лежащей на луче равного распределения.
В
рамках данного подхода можно акцентировать внимание на уменьшении степени
общественного неравнства: W(U1,U2,...,Ui,...Un)=ΣKiUi, где Кi-характеризует значимость, которую общество придает
полезности отдельных индивидов. Если увеличить К для малообеспеченных членов
общества, неравенство в распределении благ уменьшится.
=> можно подобрать значения коэффициентов т.о.,
чтобы добиться максимума общественного благосостояния при абсолютно равном
распределении полезностей. Для
двухсубъектной модели общества функция принимает вид: W=КаUa+КbUb. Необходимо подобрать значение Ka/Kb=tgα, где α-угол наклона кривой возможных полезностей, в точке,
лежащей на луче равного распределения.
3. Эгалитаристский подход.
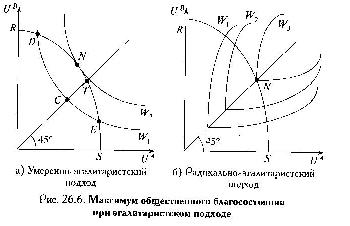 Социальная
справедливость отождествляется с равнством в распределении. (И дохода, и
полезности). Согласно эгалитаристскому подходу, чем выше степень неравенства в
распределении дохода, тем ниже при проих равных условиях уровень общественного
благосостояния.
Социальная
справедливость отождествляется с равнством в распределении. (И дохода, и
полезности). Согласно эгалитаристскому подходу, чем выше степень неравенства в
распределении дохода, тем ниже при проих равных условиях уровень общественного
благосостояния.
Умеренно
эгалитаристские предпочтения базируются на двух предпосылках:
1.благосостояние
всех индивидов равноценно для общества => для общества MRS благосостояния В благосостоянием А А(δUb/δUa)=1 во всех точках,
расположенных на луче равного распределения.
2. Чем выше степень неравенства, темы выше оценивается обществом
прирост благосостояния малообеспеченных субъектов и ниже богатых => кривые
равного благосостояния выпуклы к началу координат.
Умеренность
эгалитаризма состоит в следующем: она предполагает, что снижение благосостояния
менее обеспеченных субъектов может быть скомпенсировано ростом индивидуального
благосостояния богатых субъектов. => кривые равного благосостояния имеют равный наклон.
Эта
функция мб представлена в виде функции Кобба-Дугласа.
Радикальные галитаристские предпочтения базируются на на
предпосылке: перекрыть негативное влияние
роста неравенства на общественное благосостояние можно только в случае если
возрастет благосостояние наименее обеспеченных членов общества => кривые
равного благосостояния имеют положительный наклон и точку перелома на луче
равных благосостояний.
В
рамках обоих подходов максимум функции общественного благосостояния достигается
при Паретто-эффективном состтоянии экономики.
Радикальные
считают, что максимум общественного
благосостояния мб достигнут при абсолютно равном распределении дохода, а
умеренные признают, что с одной стороны снижение неравнства способствует росту
общественного благосостояния, а с другой-равное
распределение снижает стимулы к деловой активности, это снижает эффективность
функционирования экономики и благосостояния общества.
Вопрос 57. Характеристики общественных благ.
-неконкурентность
в потреблении (потребление индивидом этого блага не уменьшает возможностей его
потребеления другим, или MC доступа еще одного индивида к благу равны нулю.)
неделимость
в потреблении (невозможно воспрепятствовать потреблению этого блага лицами, не
желающими за него платить.)
В
действительности блага могут обладать этими свойствами в разной степени и
различных сочетаниях. Большинство благ является частными (конкурентноспособные
и присвояемые). Также существуют чистые общественные блага
(неконкурентноспособные, неприсвояемые). Пренадлежность благ, имеющих черты и
тех и других благ определяется степенью , в которой
данному благу присущ тот или иной признак.
Общественные
блага можно подразделить на потребляемые по выбору (их индивиды могут
потреблять в любом количестве в пределах выпуска) и без выбора, или обязательно(блага, поребляемые в количестве равном выпуску).Блага
первого типа могут присвояемыми и нет, а второго только неприсвояемыми.
Вопрос
58. Внешние эффекты: определение, сущность, разновидности.
Внешние
эффекты- издержки или выгоды, которые проистекают из
экономической сделки для третей стороны и не принимаются в расчет участниками
сделки. Внешний эффект имеет место если действия индивида или фирмы оказывают
влияние на благосостояние другого индивида или фирмы способом.ю
не получающим отражения в системе рыночных цен.
Типы
внешних эффектов:
-в
потреблении: связан с воздействием потребления
какого-то блага на благосостояние других
-в
производстве: связан с производством какого-то
продукта на производственные мощности
других фирм.
-потребление-производство:
когда источником эффекта являются потребители, а получателем производители
-производство-потребление-наоборот
В
зависимости от того, кто является источником внешнего эффекта он влияет
либо на функции предельных издержек и предложения (если фирма), либо на функции
предельной выгоды и спроса (если потребители).
А в зависимости от того, кто является получателем
внешнего эффекта он влияет либо на производственную функцию, либо на
функцию полезности.
Внешние
эффекты выступают одной из причин провалов рынка, те неспособность рынка
обеспечить Паретто-эффективное равновесие размещение общественных ресурсов
(аллокативную эффективность). Тк внешние
эффекты-это либо внешние издержки или выгоды, не
учтенные в функциях частных издержек ил выгод, их появление сопряжено с
возникновением разрыва либо между функциями общественных и частных совокупных
издержек, либо между функциями общественной и частной совокупной предельной
выгоды, что и приводит к Паретто-неэффективности.
Вопрос 59. Влияние разных типов внешних эффектов на эффективность.
Корректирующие налоги и субсидии Пигу.
1. Внешние эфффекты в производстве и
аллокативная эффективность.
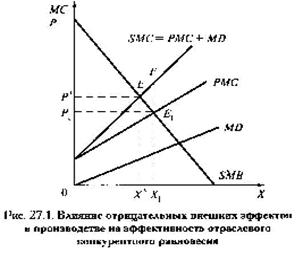 1.1.Последствия
отрицательных внешних эффектов.
1.1.Последствия
отрицательных внешних эффектов.
Отрицательные
внешние эффекты сопряжены с появлением внешних предельных издержек (MEC), или
внешнего предельного ущерба (MD), увеличивающего собственные предельные
издержки выпуска продукта (SMC) по сравнению с частными (PMC).
SMB-кривая
рыночного спроса X, отражающая предельную выгоду для потребителей от
производства каждой единицы Х.
PMC-кривая,
представляющая собой частные предельные издержки ,
полученные горизонтальным суммированием частных предельных издержек
фирм-производителей X и отражающие выплаты факторам производства. Побочным
продуктом производства Х является производство загрязняющих выбросов. MD от
загрязнения растет с ростом выпуска.
При max прибыли
будет произво диться Х1 товара,
при условии PMC=SMB.
С т.зр. общества нарвщивание выпуска должно происходить пока предельная выгода
для общества больше предельных издержек, кот вкл в себя ресурсные издержки (PMC)
и MD. Они суммируются при каждом
выпуске, те по вертикали. Парето-оптимальный выпуск, X*,
удовлетворяет условию SMC=SMB.
Выводы:
-При
наличии внешних эффектов нет оснований ожидать Паретто-оптимального размещения
общественных ресурсов.
-Эффективность
выпуска можно увеличить путем его согращения с Х1 до
Х*, и выйгрыш от такого сокращения равен S E1EF.
-Обществу
нежелательно иметь нулевой уровень загрязнения.(Это
приводит к нулевому выпуску)
-Для
применения данной модели госву дб известны реальные формы кривых спроса и
издержек, кривой MD.
 Пусть
сущ-ют две фирмы производящие соответственно продукты Xи Y,
причем производство Y оказывает
отрицательный внешний эффект на X.
Единственный фп-труд,и обе фирмы являются
ценополучателями на рынках готовой продукции и на рынке фактора. Пусть
производственная функция фирмы Y имеет
вид: Y=g(Ly),
а X: Х=f(Lx;Y).
действуя независимо при соблюдении Паретто-эффективного равновесия должно
соблюдаться равенство предельных оходностей фактора: SMPRLx=SMPRLy. Но
в силу действия внешнего эффекта уравнение приобретает вид:SMRPLy=Py*(δg/δLy)+Px*(δf/δY)*(δY/δLy).Так
как δf/δY<0,
общественная предельная доходность труда в производстве Y
меньше предельной доходности труда при производстве X.=> можно увеличить ценность выпуска
для общества, переместив часть L
из Y в Х.
Пусть
сущ-ют две фирмы производящие соответственно продукты Xи Y,
причем производство Y оказывает
отрицательный внешний эффект на X.
Единственный фп-труд,и обе фирмы являются
ценополучателями на рынках готовой продукции и на рынке фактора. Пусть
производственная функция фирмы Y имеет
вид: Y=g(Ly),
а X: Х=f(Lx;Y).
действуя независимо при соблюдении Паретто-эффективного равновесия должно
соблюдаться равенство предельных оходностей фактора: SMPRLx=SMPRLy. Но
в силу действия внешнего эффекта уравнение приобретает вид:SMRPLy=Py*(δg/δLy)+Px*(δf/δY)*(δY/δLy).Так
как δf/δY<0,
общественная предельная доходность труда в производстве Y
меньше предельной доходности труда при производстве X.=> можно увеличить ценность выпуска
для общества, переместив часть L
из Y в Х.
1.2.
Последствия положительных внеших эффетов.
В
данном случае частные издержки отчасти возвращаются обществу через внешнюю
выгоду от положительного внешнего эффекта, и кривая SMC лежит
под PMC, полученная вычетом из нее по
вертикали MB. => имеет
место занижение фактического выпуска и завышение цены, о
сравнению с общественно оптимальным уровнем.
2.
Внешние эффекты в потреблении и
аллокативная эффективность.
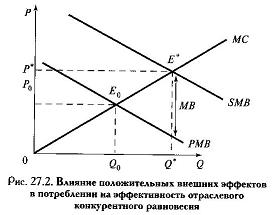
 Потребление
блага Х сопряжено с дополнительной полезностью,не
учитываемой в кривой его рыночного спроса
и отражаемой кривой внешней предельной выгоды MB.
Резтат суммирования
MB по вертикали с PMB, кривая SMB-общественной предельной выгоды.
Общественно оптимальные уровни выпуска и цены данного блага определяются точкой
E*.
Так как SMB выше, чем PMB, общественно оптимальные цена и
выпуск больше, чем в отсутствие внешнего эффекта.
Потребление
блага Х сопряжено с дополнительной полезностью,не
учитываемой в кривой его рыночного спроса
и отражаемой кривой внешней предельной выгоды MB.
Резтат суммирования
MB по вертикали с PMB, кривая SMB-общественной предельной выгоды.
Общественно оптимальные уровни выпуска и цены данного блага определяются точкой
E*.
Так как SMB выше, чем PMB, общественно оптимальные цена и
выпуск больше, чем в отсутствие внешнего эффекта.
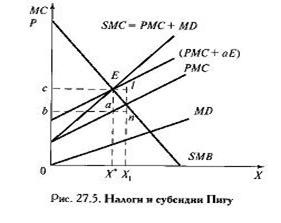
Корректирующие
налоги и субсидии Пигу.
Налог
Пигу-это налог, взимаемый с каждой единицы выпуска фирм-загрязнителей в размере
равном предельному ущербу от загрязнения приэффективном объеме выпуска. (отрезок aE),
налоговый сбор S(abcE).
При обложении производителей товара Х таким налогом их частные издержки растут
до уровня PMC+aE, и они выбирают объем выпуска
из условия:
PMC+aE=SMB
(Х*)
Субсидия
Пигу-это субсидия, выплачиваемая фирмам-загрязнителямв том же размере, что и
налог Пигу, за каждую непроизведенную ими ед
выпуска.(отрезок aE), а общая выплата субсидии-S(aEln).
Тогда производители ьудут выпускать как раз Х* продукции (эффективное
количество), тк кривая совокупных частных издержек представлена кривой PMC+aE.
Субсидии
Пигу применимы только при неизменном числе фирм в отрасли, те в SR. В LR в
отрасль могут войти новые фирмы и в итоге объем ущерба может
вырасти. Также, источником субсидий являются налоги, которые нарушают
Паретто-эффективность.
![]()
![]() следовательно Pr = C
следовательно Pr = C 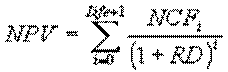 ,
,![]()
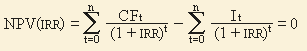
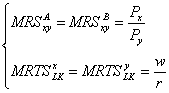
![]() (p1, p2) + p2
(p1, p2) + p2![]() (p1,
p2) º p1
(p1,
p2) º p1![]() + p2
+ p2![]()
![]() (p1,
p2) —
(p1,
p2) — ![]() ]+ p2[
]+ p2[![]() (p1,
p2) —
(p1,
p2) — ![]() ] º 0
] º 0![]() (p1, p2) + p2
(p1, p2) + p2![]() (p1,
p2) º 0.
(p1,
p2) º 0.![]() (p1, p2)
—
(p1, p2)
—![]() ]+ p2[
]+ p2[![]() (p1, p2)
—
(p1, p2)
—![]() ] º 0,
] º 0,![]() (p1, p2)
+ p2
(p1, p2)
+ p2![]() (p1, p2) º 0.
(p1, p2) º 0.![]() (p1, p2) +
(p1, p2) + ![]() (p1, p2)] + p2[
(p1, p2)] + p2[![]() (p1, p2) +
(p1, p2) + ![]() (p1, p2)] º 0,
(p1, p2)] º 0,![]() ,
, ![]() ) = 0.
) = 0. ![]() ,
, ![]() ) + p2z2(
) + p2z2(![]() ,
,![]() ) = 0.
) = 0. ![]() ,
,![]() ) = 0.
) = 0.![]() ,
,![]() ), при
которой спрос на товар 1 равняется предложению товара 1, нам гарантировано, что
спрос на товар 2 должен равняться предложению товара 2. Напротив, если мы
найдем совокупность цен, при которой спрос на товар 2 равен предложению товара
2, нам гарантировано, что рынок товара 1 будет находиться в равновесии.
), при
которой спрос на товар 1 равняется предложению товара 1, нам гарантировано, что
спрос на товар 2 должен равняться предложению товара 2. Напротив, если мы
найдем совокупность цен, при которой спрос на товар 2 равен предложению товара
2, нам гарантировано, что рынок товара 1 будет находиться в равновесии.
![]() —
— ![]() | единиц товара 1 и
приобретение в обмен |
| единиц товара 1 и
приобретение в обмен |![]() —
— ![]() | единиц товара 2. Это
означает, что B приобретает |
| единиц товара 2. Это
означает, что B приобретает |![]() —
— ![]() | товара 1 и отдает |
| товара 1 и отдает |![]() —
— ![]() | единиц товара 2.
| единиц товара 2.